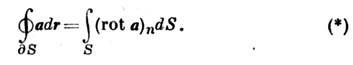СТОКСА ТЕОРЕМА — теорема, устанавливающая связь между потоком векторного поля через ориентированную поверхность с циркуляцией этого поля по краю поверхности. Л. Д. Кудрявцев … Математическая энциклопедия
Теорема Стокса — Теорема Стокса одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа. Названа в честь Дж. Г. Стокса. Содержание 1 Общая формулировка 2 … Википедия
Теорема о циркуляции магнитного поля — Теорема о циркуляции магнитного поля одна из фундаментальных теорем классической электродинамики, сформулированная Андре Мари Ампером в 1826 году. В 1861 году Джеймс Максвелл снова вывел эту теорему, опираясь на аналогии с гидродинамикой, и … Википедия
Теорема Ньютона — Лейбница — Формула Ньютона Лейбница или теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной. Если непрерывна на отрезке и ее любая первообразная на этом отрезке, то и … Википедия
Теорема Ньютона — Формула Ньютона Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной. Если непрерывна на отрезке и ее любая первообразная на этом отрезке, то имеет … Википедия
Формула Стокса — Теорема Стокса одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа. Названа в честь Дж. Г. Стокса. Содержание 1 Общая формулировка 2… … Википедия
Пи-теорема — Π теорема (пи теорема) основополагающая теорема анализа размерностей. Теорема утверждает, что если имеется зависимость между физическими величинами, не меняющая своего вида при изменении масштабов единиц в некотором классе систем единиц, то она… … Википедия
Π-теорема — основополагающая теорема анализа размерностей. Теорема утверждает, что если имеется физически значимое выражение, включающее в себя n физических переменных, и эти переменные описываются при помощи k независимых фундаментальных физических величин … Википедия
П-теорема — π теорема основополагающая теорема анализа размерностей. Теорема утверждает, что если имеется физически значимое выражение, включающее в себя n физических переменных, и эти переменные описываются при помощи k независимых фундаментальных… … Википедия
Пи теорема — π теорема основополагающая теорема анализа размерностей. Теорема утверждает, что если имеется физически значимое выражение, включающее в себя n физических переменных, и эти переменные описываются при помощи k независимых фундаментальных… … Википедия