- СТАТИСТИЧЕСКОЙ ФИЗИКИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ
- задачи, возникающие при применении математич. аппарата в статистич. физике. С. ф. м. з. в основном связаны с двумя направлениями статистич. теории: с равновесной статистич. механикой, основные математич. проблемы к-рой связаны с разработкой методов расчета средних по равновесному Гиббса распределению (см. Статистической механики математические задачи) и с неравновесной статистич. физикой, основные трудности к-рой составляют проблемы получения эволюционных уравнений для функций распределения, характеризующих систему на разных этапах ее эволюции, с последующим их решением (см., напр., Кинетическое уравнение, Броуновского движения процесс).
В задачу методов равновесной статистнч. механики входит расчет средних следующих типов (в случае использования канонич. распределения Гиббса):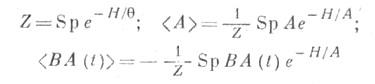
и т. д., где Н - гамильтониан системы,
 - температура, A(t) - оператор в гейзенберговском временном представлении, Z - статистич. сумма, связанная со свободной энергией системы соотношением
- температура, A(t) - оператор в гейзенберговском временном представлении, Z - статистич. сумма, связанная со свободной энергией системы соотношением 
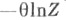 (в случае использования большого канонич. распределения вместо оператора Нфигурирует оператор
(в случае использования большого канонич. распределения вместо оператора Нфигурирует оператор  где
где  - химич. потенциал, N - число частиц, вместо Z - большая статистич. сумма, вместо F -- термодинамич. потенциал
- химич. потенциал, N - число частиц, вместо Z - большая статистич. сумма, вместо F -- термодинамич. потенциал  и т. д.). Расчет безвременных средних Zи <А> решает проблемы равновесной теории (все равновесные характеристики, такие, как внутренняя энергия, теплоемкость, уравнения состояния, статич. восприимчивости и т. д., определяются методами термодинамики, исходя из свободной энергии F), а также теории флуктуаций; расчет величин типа <ВА(t)> позволяет исследовать целый ряд динамических (зависящих от частоты) восприимчивостей системы, коэффициентов переноса и т. д.. а также исследовать особенности простейших возбуждений системы (в общем случае при
и т. д.). Расчет безвременных средних Zи <А> решает проблемы равновесной теории (все равновесные характеристики, такие, как внутренняя энергия, теплоемкость, уравнения состояния, статич. восприимчивости и т. д., определяются методами термодинамики, исходя из свободной энергии F), а также теории флуктуаций; расчет величин типа <ВА(t)> позволяет исследовать целый ряд динамических (зависящих от частоты) восприимчивостей системы, коэффициентов переноса и т. д.. а также исследовать особенности простейших возбуждений системы (в общем случае при 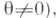 их энергию, затухание и т. д.
их энергию, затухание и т. д.
Указанные средние рассчитываются до конца только в исключительных случаях: для идеальных систем и для нек-рых специальных моделей. Эти расчеты в дальнейших исследованиях могут служить нулевым приближением. Наиболее часто рассматриваемыми моделями неидеальных статистич. систем являются системы с прямым взаимодействием частиц друг с другом (взаимодействием конечного радиуса, кулоновским взаимодействием и др.), с взаимодействием частиц с, нолем типа фотонного (в твердом теле описывающего тепловое движение кристаллич. решетки), дискретные системы типа Изинга и гейзенберговского магнетика с взаимодействием узлов конечного радиуса действия, а также сочетания взаимодействий подобных типов. В представлении вторичного квантования гамильтониан H=H0+H1 в этих случаях выражается через квадратичные комбинации операторов рождения и уничтожения (в части H0 без взаимодействия), четвертную форму (рели H1 включает прямое взаимодействие частиц), тройную форму типа используемой в квантовой электродинамике (электронфотонное взаимодействие в H1) и т. д.
Приближенные методы расчета указанных средних в большинстве случаев основываются на добавлении поправок к результатам, полученным для случая H=H0 (если нулевое приближение в физич. отношении действительно является таковым), имеющих вид явного или модифицированного разложения по степеням параметра, определяющего интенсивность взаимодействия, включенного в гамильтониан H1. При сопоставлении рассматриваемой формальной модели с реальными системами в целом ряде случаев, имеющих прикладной интерес, параметр взаимодействия, по к-рому производится лразложение
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
