СТАТИСТИЧЕСКОЙ МЕХАНИКИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ

-- совокупность общих проблем математич. физики, возникших из стремления четко осмыслить основные концепции и факты статистич. механики. Эти проблемы можно условно разделить на следующие группы:

1) обоснование основных принципов статистич. механики,
2) равновесные ансамбли в термодинамич. пределе, вывод тeрмодинамич. соотношений,
3) фазовые переходы,
4) эволюция ансамблей, проблема релаксации, исследование кинетич. и гидродинамич. уравнений,
5) основные состояния, элементарные возбуждения (в случае квантовых систем).

Статистич. механика изучает системы, состоящие из большого числа (микроскопических) частиц, заключенных внутри большой (сравнительно с характерными размерами частиц) области Vпространства Статистич. механика - в зависимости от способа описания системы - разделяется на классическую и квантовую.
Описание классич. системы, заключенной в области V, включает указание пространства Xвозможных состояний каждой отдельной частицы (одночастичное пространство), а также совокупности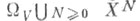 допустимых конфигураций i=1, . . ., N; N=1, 2, . . ., конечного числа частиц внутри V, задание энергии 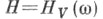для каждой конфигурации и закона эволюции системы во времени (наз. иначе динамикой), т. е. полугруппы (чаще всего группы) преобразовании U^V_t, пространства в себя, сохраняющих энергию H_V: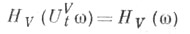

для любой и любого t. Во многих случаях пространство 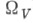бывает естественно наделено симплектич. структурой, и преобразования строятся с помощью решений т. н. гамильтоновых уравнений движения, порождаемых функцией Гамильтона H=Н _V (см. [1]). Кроме того, обычно в пространстве Xсуществует нек-рая естественная мера dx такая, что мера 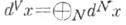в - мера в X^N )инвариантна относительно эволюции 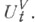Однако для макроскопич. систем, состоящих из большого числа частиц, столь детальное описание их состояний и динамики этих состояний (т. е. описание траекторий каждой отдельной частицы) оказывается малообозримым, да и бесполезным с точки зрения изучения макроскопич. свойств всей системы. Эти свойства определяются лить нек-рыми средними характеристиками конфигурации а также ее эволюции t>0 во времени: напр., долей 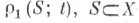частиц в конфигурации состояния к-рых принадлежат заданному множеству Sодночастичного пространства X, или долей 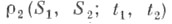частиц, состояния к-рых в момент времени t₁ принадлежат множеству а в момент t₂ - множеству и т. д.
Эти соображения привели к следующей радикальной идее: состояние макроскопич. системы следует задавать каким-либо вероятностным распределением Р на фазовом пространстве причем эволюция p_t, t>0, этого распределения во времени порождается исходной эволюцией самой системы: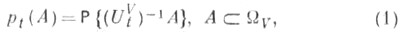

где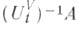 - полный прообраз множеств 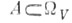при отображении Это соглашение дополняется следующим постулатом: для всякого лхорошего