- СТАТИСТИЧЕСКАЯ СУММА
функция, используемая в равновесной статистич. физике, равная нормировочной константе в выражении для плотности (или матрицы плотности - в случае квантовой системы) в каноническом гиббсовском ансамбле.
1) В случае классич. системы плотность распределения Гиббса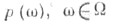
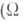- фазовое пространство системы) относительно естественной меры 
на 
задается формулой 
где
- функция Гамильтона (энергия) системы, a 
i=l, . . ., k.- нек-рый набор величин, сохраняющийся при движении системы, задаваемой гамильтонианом 
- действительные параметры. Нормировочный множитель 
и наз. С. с. (иногда статистическим интегралом или интегралом состояний). 2) В случае квантовой системы каноническое гиббсовское состояние задается матрицей плотности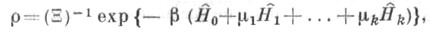
где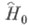
- гамильтониан (оператор энергии) системы, а 
i=1,..., k, - нек-рые коммутирующие между собой операторы, соответствующие сохраняющимся во времени величинам;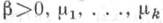 
- действительные параметры. Нормировочный множитель (наз. статистич. суммой) равен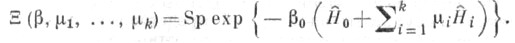 
Аналогично определяются С. с. для других гиббсовских ансамблей (микроканонического и малого канонического), а также в случае гиббсовских ансамблей, определенных для различных упрощенных модификаций реальных физич. систем (решетчатые системы, конфигурационные системы и т. д.).
В типичном случае, когда система заключена в ограниченной области
и энергия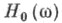 
(или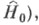 
а также другие величины 
i=l, . . ., k(соответственно операторы 
i=l, . . ., k), входящие в определение гиббсовского ансамбля, инвариантны относительно сдвигов в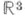 
и почти аддитивны, т. е. (в случае классич. системы) 
где
и 
- две конфигурации частиц, достаточно далеко отстоящие друг от друга (точную формулировку этого условия, а также его квантовый аналог см., напр., в [2]), в термодинамическом предельном переходе 
статистич. сумма 
имеет следующую асимптотику: 
где
- объем области 
а функция 
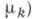- т. н. термодинамический потенциал- является важной термодинамич. характеристикой системы: с ее помощью выражаются многие другие термодинамич. характеристики (удельная энергия, плотность, удельная энтропия и т. д.). Лит.:[1] Ландау Л. Д., Лифшиц Е. М., Статистическая физика, М., 1964 (Теоретическая физика, т. 5); [2] Рюэль Д., Статистическая механика. Строгие результаты, пер. с англ., М., 1970; [3] Балеcку Р., Равновесная и неравновесная статистическая механика, пер. с англ., т. 1-2, М., 1978. Р. А. Минлос.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
