СТАБИЛЬНЫЕ И НЕСТАБИЛЬНЫЕ ТЕОРИИ

- раздел моделей теории, изучающий стабильность элементарных теорий. Пусть Т - полная теория первого порядка сигнатуры А - модель теории Ти Сигнатура получается из добавлением символов с _а выделенных элементов для всех Система <А, X> имеет сигнатуру и является обогащением модели А, в к-ром с _а интерпретируется как адля всех 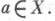Теория Т( А, X )представляет собой совокупность истинных в <A, X> формул сигнатуры 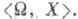Множество максимальных, совместных с Т( А, X), множеств формул сигнатуры 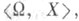не содержащих свободных переменных, отличных от нек-рого фиксированного v₀, обозначается через S( А, X). Теория Тиаз. стабильной в мощности 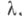если для любой модели Атеории Ти любого мощность к-рого не превосходит 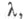мощность S( А, X )также но превосходит 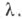Теория наз. стабильной, если она стабильна хотя бы в одной бесконечной мощности.
Пусть | Т| обозначает мощность множества формул сигнатуры Если теория Тстабильна, то она стабильна во всех мощностях, удовлетворяющих равенству 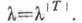Если теория Тстабильна, то существуют модель Атеории . и бесконечное множество такие, что для любой формулы сигнатуры 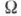и для любых двух последовательностей <a₁, . . ., а _n> <b₁, . . ., b_n> различных элементов множества Yистинность в Аэквивалентна истинности в А; при этом множество Y наз. множеством неразличимых в Тэлементов. Оказывается, что характеристич. свойством нестабильных теорий является существование множества, имеющего в определенном смысле противоположные свойства. А именно, нестабильность теории Тэквивалентна существованию формулы сигнатуры модели Атеории Ти последовательности . . . наборов элементов Атаких, что истинность 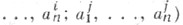в Аравносильна неравенству i<j. Поэтому нестабильны полные расширения теории линейно упорядоченных множеств, имеющие бесконечные модели, а также теория любой бесконечной булевой алгебры. В частности, нестабильна теория натуральных чисел со сложением и теория поля действительных чисел. Если теория Тнестабильна, то число типов изоморфизма моделей Тв каждой несчетной мощности равно Поэтому теория Т, категоричная в несчетной мощности стабильна. Существуют, однако, стабильные теории, не категоричные ни в какой бесконечной мощности. Такова теория T₁, сигнатура к-рой состоит из одноместного предиката и счетного множества выделенных элементов. Аксиомы этой теории утверждают, что предикат истинен на выделенных элементах и делит каждую модель T₁ на два бесконечных множества, а также что выделенные элементы не равны между собой.
Теории конечной или счетной сигнатуры, стабильные в счетной мощности, наз. также тотально трансцендентными. Всякая тотально трансцендентная теория стабильна во всех бесконечных мощностях. Всякая категоричная в несчетной мощности теория конечной или счетной сигнатуры является тотально трансцендентной. Упомянутая выше теория T₁ тотально трансцендентна. Тотально трансцендентные теории можно характеризовать и в других терминах. Пусть Т- полная теория конечной или счетной сигнатуры А - бесконечная модель теории Т. Формуле сигнатуры 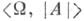припишем ранг -1, если она ложна на всех элементах модели <A, |A|>, и ранг 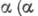- ординал), если ей не приписан никакой ранг, меньший но для каждого элементарного расширения Всистемы Аи для каждой формулы 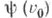сигнатуры одной из формул или приписан ранг, меньший Теория Ттогда и только тогда является тотально трансцендентной, когда для каждой модели Атеории Ткаждой формуле сигнатуры 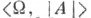приписан нек-рый ранг.

Лит.: [1] Shelah S., лAnn. of math, logic