СРЕДНЯЯ КРИВИЗНА

СРЕДНЯЯ КРИВИЗНА

поверхности Ф 2 в евклидовом трехмерном пространстве 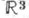- полусумма главных кривизн k1 и k2, вычисленных в точке Аэтой поверхности: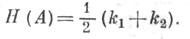

Для гиперповерхности Ф n в евклидовом пространстве эта формула обобщается следующим образом: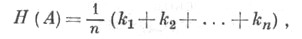


где ki, i=1, 2, . . ., п,- главные кривизны гиперповерхности, вычисленные в точке
С. к. поверхности в может быть выражена через коэффициенты первой и второй квадратичных форм этой поверхности:


где Е, F, G- коэффициенты первой квадратичной формы, L, М, N - коэффициенты второй квадратичной формы, вычисленные в точке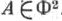 В частном случае задания поверхности уравнением z=f(z, у)С. к. вычисляется по формуле:


к-рая обобщается для гиперповерхности Ф n в заданной уравнением xn+1=f(xl,. . ., х n):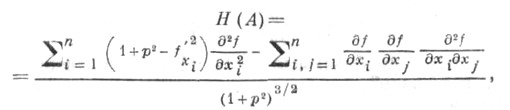


где

Л. А. Сидоров.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужна курсовая?

Смотреть что такое "СРЕДНЯЯ КРИВИЗНА" в других словарях:

  • Средняя кривизна —         поверхности в данной её точке Р, полусумма главных кривизн поверхности в этой точке (см. Дифференциальная геометрия). Если Е, F, G коэффициенты первой основной квадратичной формы поверхности, a L, М, N коэффициенты её второй основной… …   Большая советская энциклопедия

  • Средняя кривизна — …   Википедия

  • Кривизна — (матем.)         величина, характеризующая отклонение кривой (поверхности) от прямой (плоскости). Отклонение дуги MN кривой L от касательной МР в точке М можно охарактеризовать с помощью т. н. средней кривизны kcp этой дуги, равной отношению… …   Большая советская энциклопедия

  • НОРМАЛЬНАЯ КРИВИЗНА — регулярной поверхности величина, характеризующая отклонение поверхности в направлении от своей касательной плоскости в точке Р, совпадающая по абсолютной величине с кривизной соответствующего нормального сечения. Н. к. в направлении равна где k… …   Математическая энциклопедия

  • ГЛАВНАЯ КРИВИЗНА — нормальная кривизна поверхности в главном направлении, т. е. в направлении, где она достигает своего экстремального значения. Г. к. являются корнями квадратного уравнения где коэффициенты первой квадратичной формы, a L, М и N второй квадратичной… …   Математическая энциклопедия

  • Поверхностей теория —         раздел дифференциальной геометрии, в котором изучаются свойства поверхностей (см. Дифференциальная геометрия, Поверхность). В классической П. т. рассматриваются свойства поверхностей, неизменные при движениях. Одна из основных задач… …   Большая советская энциклопедия

  • Минимальные поверхности —         поверхности, у которых средняя кривизна во всех точках равна нулю (см. Кривизна). М. п. появляются при решении следующей вариационной задачи: в пространстве дана некоторая замкнутая кривая; среди всех возможных поверхностей, проходящих… …   Большая советская энциклопедия

  • ПОГРУЖЕННЫХ МНОГООБРАЗИЙ ГЕОМЕТРИЯ — теория, изучающая внешнюю геометрию и связь между внешней и внутренней . геометрией подмногообразий евклидова или риманова пространства. П. м. г. является обобщением классич. дифференциальной геометрии поверхностей в евклидовом пространстве .… …   Математическая энциклопедия

  • Скрытая масса — Космология Изучаемые объекты и процессы …   Википедия

  • Асимптотическая кривая — (асимптотическая линия) кривая на гладкой регулярной поверхности в евклидовом пространстве, в каждой точке касающаяся асимптотического направления поверхности , т.е. такого направления, в котором нормальное сечение поверхности имеет нулевую… …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»