СПЕКТР

СПЕКТР

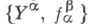прямой и обратный спектр в категории Прямым спектром в категории наз. семейство объектов с индексами из направленного множества и семейство морфизмов 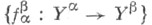из (определенных при для к-рых:


Можно определить категорию объектами к-рой служат семейства морфизмов таких, что если В этой категории морфизмом объекта 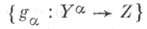в объект наз. такой морфизм категории 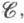что Инициальный (начальный) объект категории dir наз. пределом прямого спектра Пределы прямых спектров (прямой спектр) множеств, топологич. пространств, R-модулей являются примерами прямых спектров в соответствующих категориях.
Двойственным образом, обратным спектром в категории наз. семейство объектов с индексами из направленного множества 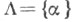и семейство морфизмов категории (определенных, если для к-рых;

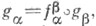Можно определить категорию объектами к-рой являются занумерованные семейства таких морфизмов что если а морфизмом объекта в объект является морфизм категории 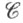такой, что при Терминальный (интегральный) объект категории наз. пределом обратного спектра 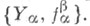Пределы обратных спектров (обратный спектр) множеств, групп, R-модулей являются пределами обратных спектров в соответствующих категориях.
Понятие обратного спектра - категорное обобщение топологич. понятия проекционного спектра.

Лит.:[1] Спеньер, Алгебраическая топология, пер. с англ., М., 1971.
М. И. Войцеховский.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем написать реферат
Синонимы:
, ,


Полезное


Смотреть что такое "СПЕКТР" в других словарях:

  • спектр — спектр, а; мн. ы, ов …   Русское словесное ударение

  • спектр — спектр, а …   Русский орфографический словарь

  • спектр — спектр/ …   Морфемно-орфографический словарь

  • спектр — а, м. spectre m. <, лат. spectrum. 1. Многоцветная полоса, получающаяся при прохождении светового луча через призму или иную преломляющую среду. БАС 1. ♦ Спектр солнечный световое изображение, получаемое на стене темной комнаты, от пропускания …   Исторический словарь галлицизмов русского языка

  • СПЕКТР — СПЕКТР, расположение ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ, упорядоченное по длине ВОЛНЫ или по ЧАСТОТЕ. Спектр видимого света является последовательностью цветов (красного, оранжевого, желтого, зеленого, голубого, синего и фиолетового). Каждый цвет… …   Научно-технический энциклопедический словарь

  • СПЕКТР — лат. spectrum, франц. spectre. а) Призрак. b) Спектр солнечный: продолговатое изображение солнца, состоящее из семи поперечных разноцветных полос. Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их корней.… …   Словарь иностранных слов русского языка

  • СПЕКТР — СПЕКТР, спектра, муж. (лат. spectrum призрак) (физ.). 1. Разноцветная полоса, получающаяся при прохождении светового луча через стеклянную призму или диффракционную решетку. Солнечный спектр или спектр солнца. Спектр Сириуса. Спектр водорода. 2.… …   Толковый словарь Ушакова

  • Спектр-Р — Спектр Р  орбитальная астрофизическая радиообсерватория. Разработана в НПО имени Лавочкина.[1] Запуск спутника планируется в конце 2010 года ракетой носителем «Зенит 2» с разгонным блоком «Фрегат СБ».[2] Первоначальные орбитальные данные… …   Википедия

  • СПЕКТР — (1) совокупность семи цветовых полос (спектральные цвета), чередующихся в определённом порядке, которые получаются при прохождении светового луча через преломляющую среду (напр. радуга, образующаяся вследствие преломления солнечных лучей в каплях …   Большая политехническая энциклопедия

  • СПЕКТР-1 — (71 402) Выпускался, гг. 1997 Масса без пассажиров, т 19,5 Макс. скорость, км/ч 75 Вместимость, чел Мест для сидения 32 Полная вместимость (8 чел./м2) 158 …   Википедия

  • СПЕКТР — (spectrum представление, образ) в физике, совокупность всех значений какой либо физической величины, характеризующей систему или процесс. Чаще всего пользуются понятиями частотного спектра колебаний. Наиболее подробно изучены спектры… …   Современная энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»