- СКОЛЬЗЯЩЕГО СРЕДНЕГО ПРОЦЕСС
- стационарный в широком смысле случайный процесс, к-рый может быть получен с помощью применения нек-рого линейного преобразования к процессу с некоррелированными значениями (т. е. к процессу белого шума). Часто С. с. п. наз. также более частный процесс X(t).с дискретным временем t =0, +1, . . . , представимый в виде
 (1)
(1)
где
 - символ Кронекера (так что Y(t) - процесс белого шума со спектральной плотностью s2/2p), q- нек-рое целое положительное число, a b1, . . . , bq - постоянные коэффициенты. Спектральная плотность f(l).такого С. с. п. определяется формулой
- символ Кронекера (так что Y(t) - процесс белого шума со спектральной плотностью s2/2p), q- нек-рое целое положительное число, a b1, . . . , bq - постоянные коэффициенты. Спектральная плотность f(l).такого С. с. п. определяется формулой
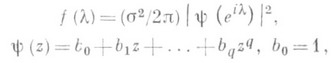
а его корреляционная функция
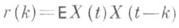 имеет вид
имеет вид

Обратно, если корреляционная функция r(k).стационарного процесса X(t).с дискретным временем tобладает тем свойством, что r(k)=0 при |k|>q для какого-то целого положительного q, то X(t) - это С. с. п. порядка q, т. <е. <он допускает представление вида (1), где Y(t) - белый шум (см., напр., [1], § 5.7).
Наряду со С. с. п. конечного порядка q, представимыми в виде (1), существуют также два типа С. с. п. с дискретным временем бесконечного порядка, а именно: односторонние С. с. п., допускающие представление вида
 (2)
(2)
где Y(t).- белый шум, а ряд в правой части (2) сходится в среднем квадратичном (и, значит,

 ), и более общие двусторонние С. с. п., представимые в виде
), и более общие двусторонние С. с. п., представимые в виде
 (3)
(3)
где Y(t) - белый шум, а
 . Класс двусторонних С. с. н. совпадает с классом стационарных процессов X(t), имеющих спектральную плотность f(l), а класс односторонних C. с. п.- с классом процессов, имеющих спектральную плотность f(l) такую, что,
. Класс двусторонних С. с. н. совпадает с классом стационарных процессов X(t), имеющих спектральную плотность f(l), а класс односторонних C. с. п.- с классом процессов, имеющих спектральную плотность f(l) такую, что,

(см. [2], |1], |3]).
Односторонним или соответственно двусторонним С. с. и. с непрерывным временем наз. стационарный процесс
 , представимый в виде
, представимый в виде
 ,
,
или соответственно в виде
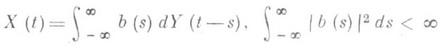 ,
,
где
 , т. е. Y'(t)-обобщенный процесс белого шума. Класс двусторонних С. с. п. с непрерывным временем совпадает с классом стационарных процессов X(t), имеющих спектральную плотность f(l)), а класс односторонних С. с. п. с непрерывным временем- с классом процессов, имеющих такую спектральную плотность f(l), что
, т. е. Y'(t)-обобщенный процесс белого шума. Класс двусторонних С. с. п. с непрерывным временем совпадает с классом стационарных процессов X(t), имеющих спектральную плотность f(l)), а класс односторонних С. с. п. с непрерывным временем- с классом процессов, имеющих такую спектральную плотность f(l), что
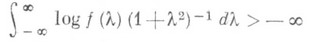
(см. [4], [3], [5]).
Лит.:[1] Андерсон Т., Статистический анализ временных рядов, пер. с англ., М., 1976; [2] Колмогоров А. Н., "Бюлл. Моск. гос. ун-та", 1941, т. 2, в. 6, с. 1-40; [3] Дуб Дж., Вероятностные процессы, пер. с англ., М., 1956; [4] Каrhunen К.,"Ann. Acad. Sci. Fennicae. Ser. A. Matli.-Phys.", 1947, As 37, p. 3 - 79; [5] Розанов Ю. А., Стационарные случайные процессы, М., 1963. А. М. Яглом,
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
