СИМПЛЕКТИЧЕСКАЯ ГРУППА

одна из классических групп, определяемая как группа автоморфизмов знакопеременной билинейной формы Ф на левом К-модуле Е, где К - коммутативное кольцо. В случае, когда Е=К ^2т и матрица формы Ф в канонич. базисе {е _i} модуля Еимеет вид

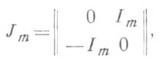
где I _т- единичная матрица порядка т, соответствующая С. г. называется С. г. от 2т переменных над кольцом Ки обозначается Sp(m, К).или Sp_2m(K). Матрица любого автоморфизма из Sp_2m(K) в базисе {е _i} наз. симплектической матрицей. Пусть К - поле и Ф - невырожденная знакопеременная билинейная форма в n-мерном векторном пространстве Енад К. Тогда пчетно, ассоциированная с формой Ф С. г., изоморфная группе Sр _n(K), порождается всевозможными линейными преобразованиями пространства Евида s_e,a,

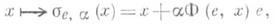
где 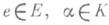. Линейные преобразования вида s_e,a наз. симплектическими трансвекциями, или сдвигами, в направлении прямой Ке. Центр Z группы Sр _n(K) состоит из матриц I_n и - I_n, если char ; если же char K=2, то Z={I _п}. Факторгруппа Sp_n(K)/Z наз. проективной симплектической группой и обозначается РSр _n(K). Все проективные С. г. просты за исключением

к-рые изоморфны соответственно симметрич. группам S₃ и S₆ и знакопеременной группе A₄ (через F_q обозначено поле из qэлементов). Порядок С. г. Sp_2m (F_q).равен

С. г. Sр ₂(K) совпадает со специальной линейной группой SL₂ (К);если char 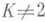, то группа PSp₄ (К).изоморфна факторгруппе группы W₅(K, f) по ее центру (где W₅(K, f) - коммутант ортогональной группы симметрической билинейной формы f от пяти переменных индекса 2).

За исключением случая т=2,char K=2, всякий автоморфизм j группы Sp_2m (К).может быть представлен в виде

где t - автоморфизм поля 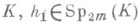и h₂ - ли-

нейное преобразование пространства Е, представляющееся в базисе {е _i} матрицей вида

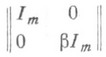
(b - ненулевой элемент поля К).

С. г. Sр _2m (К).совпадает с группой K-точек линейной алгебраич. группы Sp_2m, задаваемой уравнением 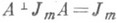. Эта алгебраич. группа, тоже называемая С. г., является простой односвязной линейной алгебраич. группой типа С _m, ее размерность равна 2т ²+т.

В случае, когда или 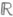, С. г. Sp_2m (К).есть связная односвязная простая комплексная (соответственно вещественная) группа Ли. Группа является одной из вещественных форм комплексной С. г. . Остальные вещественные формы этой группы тоже иногда называют С. г. Это - подгруппы

, выделяемые из группы условием сохранения эрмитовой формы вида

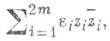
где e_i=1 при и и e_i=-1 при остальных i. Группа Sp (0, т) - компактная вещественная форма комплексной С. г. . С. г. Sp(p, q).изоморфна группе всех линейных преобразований правого векторного пространства 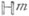над телом кватернионов 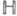размерности т=р+q, к-рые сохраняют кватернионную эрмитову форму индекса min(p, q), то есть форму вида

где

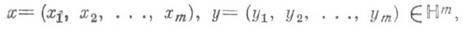
а черта означает переход к сопряженному кватерниону.

Лит.:[l] Apтин Э., Геометрическая алгебра, пер. с англ., М., 1969; [2] Бурбаки Н., Алгебра. Модули, кольца, формы, пер. с франц., М., 1966; [3] Дьёдонне Ж., Геометрия классических групп, пер. с франц., М., 1974; [4] Xелгасон С., Дифференциальная геометрия и симметрические пространства, пер. с англ., М., 1964; [5] Шевалле К., Теория групп Ли, пер. с англ., т. 1, М., 1948. В. Л. Попов.