СИЛЬНО НЕПРЕРЫВНАЯ ПОЛУГРУППА

семейство линейных ограниченных операторов T(t), t>0, в банаховом пространстве X, обладающее свойствами:

1)

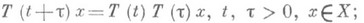
2) функции Т(t)xнепрерывны на

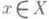
при любом

При выполнении 1) из измеримости всех функций , и, в частности, из односторонней (справа или слева) слабой непрерывности следует сильная непрерывность T(t). Для С. н. п. конечное число

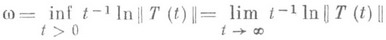
наз. т и п о м п о л у г р у п п ы. Таким образом, нормы всех функций Т(t)xрастут на 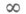не быстрее экспоненты 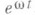. Классификация С. н. п. основана на их поведении при . Если существует такой ограниченный оператор J, что 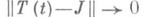при 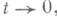то J - проекционный оператор и 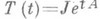, где А - ограниченный линейный оператор, коммутирующий с J. В этом случае Т(t)непрерывна по норме операторов. Если J=J, то ,- равномерно непрерывная группа операторов.

Если 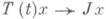при каждом 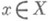, то J- также проекционный оператор, проектирующий Xна подпространство Х ₀ - замыкание объединения всех значений .

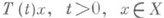Для того чтобы J существовал и равнялся J, необходимо и достаточно, чтобы 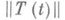была ограничена на (0,1) и чтобы Х ₀=Х. В этом случае полугруппа T(t),доопределенная равенством T(0)=I, сильно непрерывна при (удовлетворяет С ₀ -у с л о в и ю). Для более широких классов полугрупп предельное соотношение 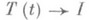выполняется в обобщенном смысле:

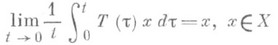
(суммируемость по Чезаро, С ₁ -у с л о в и е), или

(суммируемость по Абелю, А-условие). При этом предполагается, что функции 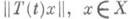, интегрируемы на [0,1] (а значит, и на любом конечном отрезке).

Поведение С. н. п. при 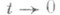может быть совсем нерегулярным. Напр., функции 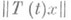могут иметь при t=0степенную особенность.

Для плотного в Х ₀ множества элементов хфункции Т(t)xдифференцируемы на 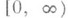. Важную роль играют С. н. п., для к-рых функции Т(t)xдифференцируемы при всех хдля t>0. В этом случае оператор Т'(t)ограничен при каждом tи его поведение при 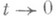дает новые возможности для классификации полугрупп. Выделены классы С. н. п., для к-рых Т(t)допускает голоморфное продолжение в сектор комплексной плоскости, содержащий полуось .

См. Полугруппа операторов, Производящий оператор полугруппы.

Лит.:[1] X и л л е Э., Ф и л л и п с Р., Функциональный анализ и полугруппы, пер. с англ., М., 1962. С. Г. Крейн.