РОД КРИВОЙ

- численный инвариант одномерного алгебраич. многообразия, определенного над полем k. Род g гладкой полной алгебраич. кривой Xравен размерности пространства регулярных дифференциальных 1-форм на X. Род алгебраич. кривой X, по определению, равен роду полной гладкой алгебраич. кривой, бирационально изоморфной кривой X. Для любого целого существует алгебраич. кривая рода g. Алгебраич. кривая над алгебраически замкнутым полем рода g=0 является рациональной кривой, т.. е. бирационально изоморфна проективной прямой Р ¹. Кривые рода g=1. (эллиптич. кривые) бирационально изоморфны гладким кубич. кривым в Р ². Алгебраич. кривые рода g> 1 распадаются на два класса: гиперэллиптич. кривые и негиперэллиптич. кривые. Для негиперэллиптич. 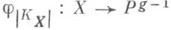кривых Xрациональное отображение , определяемое канонич. классом K_X полной гладкой кривой, является изоморфным вложением. Для гиперэллиптич. кривой Xотображение является двулистным накрытием рациональной кривой 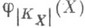, разветвленным в 2g+2 точках.

Если X - проективная плоская кривая степени т, то

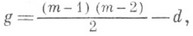
где d - неотрицательное целое число, измеряющее отклонение от гладкости кривой X. Если Xимеет только обыкновенные двойные особые точки, то d равно числу особых точек алгебраич. кривой X. Для пространственной кривой Xимеет место оценка

где т- степень кривой Xв Р ³.

Если 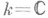- поле комплексных чисел, то алгебраич. кривая X может быть рассмотрена как риманова поверхность. В этом случае гладкая полная кривая Xрода gгомеоморфна сфере с gручками.

Лит.:[1] Ш а ф а р е в и ч И. Р., Основы алгебраической геометрии, М., 1972; [2] Х а р т с х о р н Р., Алгебраическая геометрия, пер. с англ., М., 1981. Вик. С. Куликов.