- РАНГОВАЯ СТАТИСТИКА
- статистика, построенная по вектору рангов. Если R=(R1,... , Rn) - рангов вектор, построенный по случайному вектору наблюдений Х= (Х 1, ... , Х п), то любая статистика Т=Т(R), являющаяся функцией от R, наз. р а н г ов о й с т а т и с т и к о й. Классич. пример Р. с. дает коэффициент
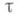 р а н г о в о й к о р р е л яц и и К е н д а л л а между векторами Rи 1 = (1, 1, ... , 1), к-рый определяется по формуле
р а н г о в о й к о р р е л яц и и К е н д а л л а между векторами Rи 1 = (1, 1, ... , 1), к-рый определяется по формуле

В классе всех Р. с. особое положение занимают т. <н. линейные Р. с., к-рые определяются следующим образом. Пусть
 - произвольная квадратная матрица порядка п. Тогда статистика
- произвольная квадратная матрица порядка п. Тогда статистика

наз. л и н е й н о й р а н г о в о й с т а т и с т и к о й. Напр., к о э ф ф и ц и е н т r р а н г о в о й к о р р ел я ц и и С п и р м е н а между векторами Rи 1, определяемый по формуле

является линейной Р. с.
Линейные Р. с., как правило, просто устроены в вычислительном отношении и их распределения вероятностей нетрудно находить. Именно поэтому в теории Р. с. играет большую роль понятие проекции Р. с. в семейство линейных Р. с. Если Т - нек-рая Р. с., построенная по случайному вектору X, относительно распределения вероятностей к-рого высказана гипотеза H0, то п р о е к ц и е й
 Р. с. T в семейство линейных Р. с. наз. такую линейную Р. с., что
Р. с. T в семейство линейных Р. с. наз. такую линейную Р. с., что  минимально при справедливости H0. Как правило, проекция
минимально при справедливости H0. Как правило, проекция
 достаточно хорошо аппроксимирует Р. с. Т, и разность
достаточно хорошо аппроксимирует Р. с. Т, и разность 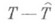 пренебрежимо мала, когда
пренебрежимо мала, когда 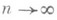 . При справедливости гипотезы H0, согласно к-рой компоненты Х 1,... , Х n случайного вектора Xсуть независимые случайные величины, проекция
. При справедливости гипотезы H0, согласно к-рой компоненты Х 1,... , Х n случайного вектора Xсуть независимые случайные величины, проекция  Р. с. Топределяется по формуле
Р. с. Топределяется по формуле
 (*)
(*)
где
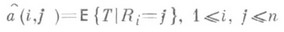 (см. [1]).
(см. [1]).
Существует внутренняя связь между Р. с.
 и
и 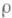 . Как показано в [1], при справедливости гипотезы H0 проекция
. Как показано в [1], при справедливости гипотезы H0 проекция 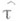 коэффициента корреляции Кендалла
коэффициента корреляции Кендалла 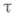 в семейство линейных Р. с. с точностью до постоянного множителя совпадает с коэффициентом ранговой корреляции Спирмена
в семейство линейных Р. с. с точностью до постоянного множителя совпадает с коэффициентом ранговой корреляции Спирмена  , а именно:
, а именно:
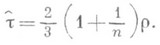
Из этого равенства следует, что коэффициент корреляции соrr
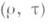 между
между 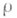 и
и 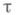 равен
равен
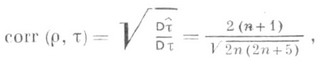
т. е. при больших пР. с.
 и
и 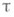 асимптотически эквивалентны (см. [2]).
асимптотически эквивалентны (см. [2]).
Лит.:[1] Г а е к Я., Ш и д а к З., Теория ранговых критериев, пер. с англ., М., 1971; [2] К е n d a l l M. G., Rank correlation methods, 4ed., L., 1970. М. С. Никулин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
