- БЕССЕЛЯ НЕРАВЕНСТВО
-
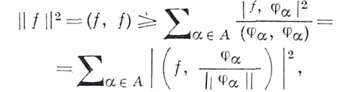
где
 - элемент (пред)гильбертова пространства Нсо скалярным произведением
- элемент (пред)гильбертова пространства Нсо скалярным произведением  -ортогональная система ненулевых элементов из Н. Правая часть Б. в. при любой мощности множества индексов Асодержит не более счетного числа слагаемых, отличных от нуля. Б. н. вытекает из тождества Бесселя
-ортогональная система ненулевых элементов из Н. Правая часть Б. в. при любой мощности множества индексов Асодержит не более счетного числа слагаемых, отличных от нуля. Б. н. вытекает из тождества Бесселя
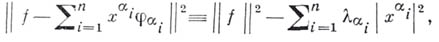
справедливого для любой конечной системы элементов
 В этой формуле
В этой формуле 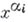 - коэффициенты Фурье вектора f по ортогональной системе
- коэффициенты Фурье вектора f по ортогональной системе 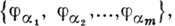 т. е. числа
т. е. числа
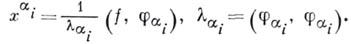
Геометрически Б. н. означает, что ортогональная проекция элемента f на линейную оболочку элементов
 ,
, 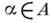 , имеет норму, не превосходящую нормы
, имеет норму, не превосходящую нормы  (т. е. гипотенуза не короче катета). Для того чтобы вектор
(т. е. гипотенуза не короче катета). Для того чтобы вектор  принадлежал замкнутой линейной оболочке векторов
принадлежал замкнутой линейной оболочке векторов 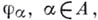 необходимо и достаточно, чтобы Б. н. обращалось в равенство. Если это имеет место при любом
необходимо и достаточно, чтобы Б. н. обращалось в равенство. Если это имеет место при любом  , то говорят, что для системы
, то говорят, что для системы 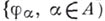 в
в  выполняется Ларсеваля равенство.
выполняется Ларсеваля равенство.
Для системы
 линейно независимых (не обязательно ортогональных) элементов из Нтождество Бесселя и Б. н. принимают вид
линейно независимых (не обязательно ортогональных) элементов из Нтождество Бесселя и Б. н. принимают вид
где
 - элементы матрицы, обратной к матрице Грама (см. Грама определитель).первых пвекторов исходной системы.
- элементы матрицы, обратной к матрице Грама (см. Грама определитель).первых пвекторов исходной системы.
Б. н. предложено Ф. Бесселем (F. Bessel) в 1828 для тригонометрич. системы.
Лит..-41 ] Кудрявцев Л. Д., Математический анализ, 2 изд.,.т 2; М., 1973. Л. П. Купцов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
