БЕСКОНЕЧНО УДАЛЕННЫЕ ЭЛЕМЕНТЫ

несобственные элементы,- элементы (точки, прямые, плоскости и т. д.), возникающие при расширении нек-рого аффинного пространства до компактного пространства. Б. у. э. являются одной из форм проявления в различных математич. теориях "актуальной" бесконечности. При этом неразрывная связь бесконечного и конечного проявляется в том, что Б. у. э. имеют смысл лишь постольку, поскольку они рассматриваются при нек-рой конкретной компактификации данного "конечного" пространства. Ниже описываются виды Б. у. э., возникающие при наиболее часто применяемых способах компактификации евклидовых конечномерных пространств.

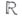1) Введением Б. у. э. (точек ) числовая прямая пополняется до компактной расширенной числовой прямой 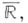гомеоморфной отрезку. Другой способ компактификации состоит в погружении в действительную проективную прямую 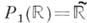, гомеоморфную окружности (см. Проективное пространство);при этом 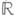пополняется одной единственной бесконечно удаленной точкой .

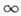2) Добавлением одной единственной бесконечно удаленной точки 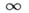конечная комплексная плоскость 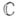пополняется до компактной расширенной комплексной плоскости 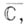гомеоморфной комплексной проективной прямой или Римана сфере (единичной сфере в евклидовом пространстве ).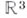

3) Добавлением одной единственной бесконечно удаленной точки n-мерное действительное числовое пространство пополняется до компактного расширенного числового пространства 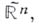гомеоморфного сфере 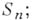этот гомеоморфизм наглядно демонстрируется стереографической проекцией. Другой способ компактификации состоит в погружении 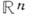в n-мерное действительное проективное пространство . При 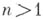эти две компактификации не гомео-морфны.

Например, параллельным прямым в проективной плоскости 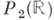соответствует одна и та же бесконечно удаленная точка, непараллельным прямым - различные бесконечно удаленные точки. Все бесконечно удаленные точки плоскости составляют бесконечно удаленную прямую. Аналогично, в проективном пространстве P₃(R) каждая плоскость дополнена бесконечно удаленной прямой. Все бесконечно удаленные точки и бесконечно удаленные прямые в составляют бесконечно удаленную плоскость. Вообще, в все Б. у. э. размерности составляют бесконечно удаленную 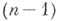-мерную гиперплоскость.

4) Компактификация комплексного n-ме. <рного числового пространства 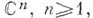также возможна посредством погружения 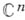в комплексное n-мерное проективное пространство . В также все Б. у. э. размерности составляют комплексную 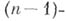мерную бесконечно удаленную гиперплоскость. Другой способ компактификации состоит в расширении 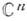до расширенного комплексного пространства представляющего собой топологич. произведение n пространств При 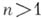пространства 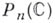и не гомеоморфны. 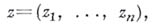Бесконечно удаленными точками пространства являются те наборы в к-рых хотя бы одна координата . Множество всех бесконечно удаленных точек пространства естественно разбивается на пмножеств

причем каждое 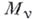имеет размерность 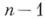. Точка 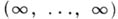принадлежит всем 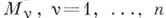. При рассмотрении действительных функций в 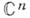применима также одноточечная компактификация , гомеоморфная или сфере .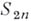

Лит.:[1] Вурбаки Н., Общая топология. Топологические группы. Числа и связанные с ними группы и пространства, пер. с франц., М., 1969; [2] Ефимов Н. В., Высшая геометрия, 5 изд., М., 1971;[3]Хартсхорн Р., Основы проективной геометрии, пер. с англ., М., 1970; [4] Фукс Б. А., Введение в теорию аналитических функций многих комплексных переменных, М., 1962; [5] Шабат Б. В., Введение в комплексный анализ, 2 изд., ч. 1-2, М., 1976. Е. Д. Соломениев.