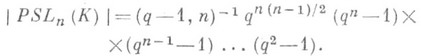Проективная группа — от переменных над телом группа преобразований мерного проективного пространства , индуцированных невырожденными линейными преобразованиями пространства . Имеется естественный эпиморфизм … Википедия
Полная проективная группа — Проективная группа от n переменных над телом K группа PGLn(K) преобразований (n − 1) мерного проективного пространства Pn − 1(K), индуцированных невырожденными линейными преобразованиями пространства Kn. Имеется естественный эпиморфизм , ядром… … Википедия
Унимодулярная проективная группа — Проективная группа от n переменных над телом K группа PGLn(K) преобразований (n − 1) мерного проективного пространства Pn − 1(K), индуцированных невырожденными линейными преобразованиями пространства Kn. Имеется естественный эпиморфизм , ядром… … Википедия
ПРОЕКТИВНАЯ НОРМАЛЬ — обобщение понятия нормали в метрич. геометрии. В отличие от последней, где нормаль вполне определяется касательной плоскостью к поверхности (т. е. окрестностью первого порядка), в проективной геометрии это не так. Даже и члены третьего порядка… … Математическая энциклопедия
Проективная плоскость — Проективная плоскость двумерное проективное пространство. Проективная плоскость отличается важной ролью, которую играет т. н. аксиома Дезарга, в проективных пространствах больших размерностей являющаяся теоремой. Проективная плоскость… … Википедия
ПРОЕКТИВНАЯ ПЛОСКОСТЬ — двумерное проективное пространство, инцидентностная структура , где элементы множества наз. точкам и, элементы множества прямыми, а I отношение инцидентности. Инцидентностная структура удовлетворяет следующим аксиомам: 1) для любых двух различных … Математическая энциклопедия
Проективная геометрия — раздел геометрии, изучающий свойства фигур, не меняющихся при проективных преобразованиях (См. Проективное преобразование), например при проектировании. Такие свойства называются проективными. Параллельность и перпендикулярность прямых,… … Большая советская энциклопедия
ПРОЕКТИВНАЯ ПРЯМАЯ — проективное пространство размерности 1; П. п., рассматриваемая как самостоятельный объект, является замкнутым одномерным многообразием. П. п. является своеобразным проективным пространством на ней нет интересных отношений инцидентности, как у… … Математическая энциклопедия
ПОЛНАЯ ЛИНЕЙНАЯ ГРУППА — группа всех обратимых матриц степени пнад ассоциативным кольцом K с единицей; общепринятое обозначение: GLn(K).или GL(n, К). П. л. г. GL(n, K) может быть также определена как группа автоморфизмов АutK(V) свободного правого K модуля Vс… … Математическая энциклопедия
ПРОЕКТИВНАЯ ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, изучающий дифференциально геометрические свойства кривых и поверхностей, сохраняющихся при проективных преобразованиях. Таковы, напр., понятия асимптотич. направления или, более общо, сопряженных направлений, соприкасающейся… … Математическая энциклопедия
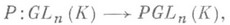ядром к-рого служит группа гомотетий пространства К n, изоморфная мультипликативной группе Z* центра Z тела К. Элементы группы PGLn(K), наз. проективными преобразованиями, являются коллинеациями пространства Р п-1 (К). Наряду с группой PGLn (К), наз. также полной проективной группой, рассматривают унимодулярную проективную группу PSLn (К). и вообще группы вида P(G), где G - нек-рая линейная группа.
группа PSLn (К).проста, за исключением двух случаев, когда n=2 и |K|=2 или 3. Если К - конечное поле из qэлементов, то 
