- ПРЕДСТАВЛЕНИЕ СО СТАРШИМ ВЕКТОРОМ
линейное представление r конечномерной полупростой расщепляемой алгебры Ли
 над полем kхарактеристики нуль с расщепляющей Картана подалгеброй t, удовлетворяющее следующим условиям.
над полем kхарактеристики нуль с расщепляющей Картана подалгеброй t, удовлетворяющее следующим условиям.
1) В пространстве Vпредставления r существует циклический вектор v (т. е. V - наименьшее
 -инвариантное подпространство, содержащее v).
-инвариантное подпространство, содержащее v).
2) p(h)(v)=h(h)vдля всех
 , где l- некоторая фиксированная линейная форма на t со значениями в k.
, где l- некоторая фиксированная линейная форма на t со значениями в k.
3) Если a1,...,ar- система простых корней, определенная век-рым лексикографич. упорядочением множества D всех корней алгебры
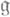 относительно t (см. Корневая система), а
относительно t (см. Корневая система), а  - соответствующие корню а; векторы из базиса Шевалле алгебры
- соответствующие корню а; векторы из базиса Шевалле алгебры
 для всех i=1, . . ., r.
для всех i=1, . . ., r.
Таким образом, l является весом относительно сужения r на t (см. Вес представления); он наз. старшим весом. Пространство Vназ. циклическим
 -модулем со старшим весом l и образующей v, a v наз. старшим вектором.
-модулем со старшим весом l и образующей v, a v наз. старшим вектором.
Для всякой линейной формы l на t существует единственное с точностью до эквивалентности неприводимое представление rl алгебры
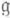 со старшим весом l.
со старшим весом l.  -модуль V(l), определяемый rl, является прямой суммой весовых подпространств относительно сужения rl на t. Их веса имеют вид
-модуль V(l), определяемый rl, является прямой суммой весовых подпространств относительно сужения rl на t. Их веса имеют вид

где ni- целые неотрицательные числа. Весовое подпространство Vm(l) веса m конечномерно, натягивается над kна векторы вида

и для любого
 ограничение rl(h) на Vm (К).является скалярным оператором умножения на m(h). Пространство Vl(l) одномерно; вес lявляется единственным старшим весом представления rl и может быть охарактеризован как единственный вес t-модуля V(l) такой, что любой другой вес имеет вид
ограничение rl(h) на Vm (К).является скалярным оператором умножения на m(h). Пространство Vl(l) одномерно; вес lявляется единственным старшим весом представления rl и может быть охарактеризован как единственный вес t-модуля V(l) такой, что любой другой вес имеет вид
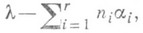
где ni - целые неотрицательные числа.
Представление rl конечномерно тогда и только тогда, когда l - доминантная линейная форма на t, то есть
 - целое неотрицательное число для всех i=1, . . ., r. Всякое неприводимое конечномерное линейное представление алгебры
- целое неотрицательное число для всех i=1, . . ., r. Всякое неприводимое конечномерное линейное представление алгебры  имеет вид rl, для нек-рой доминантной линейной формы Кна t (так что все такие представления классифицируются с точностью до эквивалентности доминантными линейными формами на t). Множество всех весов конечномерного представления rl, относительно t инвариантно относительно Вейля группы алгебры
имеет вид rl, для нек-рой доминантной линейной формы Кна t (так что все такие представления классифицируются с точностью до эквивалентности доминантными линейными формами на t). Множество всех весов конечномерного представления rl, относительно t инвариантно относительно Вейля группы алгебры 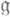 (рассматриваемой как группа линейных преобразований пространства t), и если веса m и g лежат в одной орбите группы Вейля, то размерности пространств Vm(l). и Vg(l) совпадают. Для всякого веса m. и всякого корня
(рассматриваемой как группа линейных преобразований пространства t), и если веса m и g лежат в одной орбите группы Вейля, то размерности пространств Vm(l). и Vg(l) совпадают. Для всякого веса m. и всякого корня
 число m (ha) - целое; если при этом m+a- тоже вес, то
число m (ha) - целое; если при этом m+a- тоже вес, то 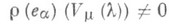 (здесь ha - элемент из t, соответствующий a, а е a- корневой вектор корня a).
(здесь ha - элемент из t, соответствующий a, а е a- корневой вектор корня a).
Лит.:[1] Джекобсон Н., Алгебры Ли, пер. с англ., М., 1964; [2] Теория алгебр Ли. Топология групп Ли. Семинар "Софус Ли", пер. с франц., М., 1962; [3] Желобенко Д. П., Компактные группы Ли и их представления, М., 1970; [4] Cartan В., "Bull. sci. math.", 1925, t. 49, p. 130-52; L5] Harish-Chandra, "Trans. Amer. Math. Soc.", 1951, V. 70, p. 28-96. В. Л. Попов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
