ПРЕДЕЛ

- одно из основных понятий математики, означающее, что какая-то переменная, зависящая от другой переменной, при определенном изменении последней, неограниченно приближается к нек-рому постоянному значению. Основным при определении П. является понятие близости рассматриваемых объектов: только после его введения П. приобретает точный смысл. С П. связаны основные понятия математич. анализа: непрерывность, производная, дифференциал, интеграл. Одним из простейших случаев П. является П. последовательности.

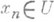Предел последовательности. Пусть X - топологич. пространство. Последовательность его точек х _n, n=1, 2, ... , наз. сходящейся к точке или, что то же самое, точка х ₀ наз. пределом данной последовательности, если для любой окрестности Uточки х ₀ существует такое натуральное N, что для всех n>N выполняется включение ; при этом пишут

В случае, когда X - хаусдорфово пространство, П. последовательности 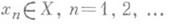, если он существует, единствен. Для метрич. пространства Xточка х ₀ является П. последовательности {х _n} тогда и только тогда, когда для любого e>0 существует такое натуральное N, что для всех номеров n>N выполняется неравенство r(x_n, x₀)<e, где r( х _п, х ₀) - расстояние между точками х _п и х ₀. Если последовательность точек метрич. пространства сходится, то она ограничена. Последовательность точек полного метрич. пространства является сходящейся в том и только в том случае, когда она фундаментальная. В частности, это верно для числовых последовательностей, для к-рых исторически впервые возникло понятие П. последовательности. Для числовых последовательностей справедливы формулы

с - произвольное фиксированное число,

а если то

Эти свойства числовых последовательностей переносятся на П. последовательностей более общих структур, напр, свойство П. суммы - на последовательности точек линейных топологич. пространств, свойства П. произведения - на последовательности точек топологич. групп и т. д.

Если действительные числовые последовательности и сходятся и , n=1, 2, ... , то

т. е. при предельных переходах нестрогие неравенства сохраняются. Если

и , то последовательность z_n, n=l, 2, ... , сходится к тому же П.: 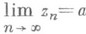. Эти свойства обобщаются на П. последовательностей точек упорядоченных множеств.

Всякая возрастающая (убывающая) последовательность действительных чисел х _п, т. е. такая, что х _п х _п+1 (соответственно х _п х _n+1), n=1, 2, ... , ограниченная сверху (снизу), сходится, и ее П. является верхняя (нижняя) грань множества ее значений. Напр., если а>0, k - натуральное число, а _п - приближенное значение корня с пдесятичными знаками после запятой, вычисленное с недостатком, то а _п, п=1,2, ... , образуют возрастающую последовательность и Другим примером возрастающей ограниченной сверху последовательности является последовательность периметров правильных многоугольников с псторонами, n=3, 4, ... , вписанных в нек-рую окружность, к длине к-рой и сходится эта последовательность.

Особую роль в теории числовых последовательностей играют бесконечно малые последовательности, т. <е. последовательности, сходящиеся к нулю. Общее понятие П. числовой последовательности сводится к понятию бесконечно малой в том смысле, что числовая последовательность сходится к нек-рому числу в том и только в том случае, когда разность между членами последовательности и этим числом является бесконечно малой последовательностью.

Полезным является и понятие бесконечно больших числовых последовательностей, т. е. последовательностей, имеющих своим П. либо одну из бесконечностей со знаком или , либо бесконечность без знака . Для определения бесконечных П. вводятся понятия e-окрестностей, e>0, бесконечностей , и в множестве действительных чисел по формулам

н понятие e-окрестности в множестве комплексных чисел :

Пишут

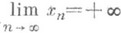(соответственно или 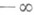), 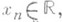n=1, 2, ... , если для любого e>0 существует такой номер N, что для всех номеров n>N выполняется включение (соответственно включение 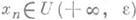или ). Аналогично определяется бесконечный П. для последовательностей комплексных чисел.

Из всякой ограниченной числовой последовательности можно выделить сходящуюся подпоследовательность (см. Болъцано- Вейерштрасса теорема), а из всякой неограниченной - бесконечно большую.

П. (конечный или бесконечный) какой-либо подпоследовательности данной последовательности наз. частичным пределом последней. В множестве всех частичных П. всякой последовательности действительных чисел всегда имеются как наибольший, так и наименьший (конечные или бесконечные). Наибольший (соответственно наименьший) частичный П. последовательности наз. ее верхним (соответственно нижним) пределом. Последовательность имеет конечный или бесконечный П. тогда и только тогда, когда ее верхний П. совпадает с нижним, причем их общее значение и является П.

С помощью П. последовательности могут быть определены другие понятия П., напр. П. функции и П. интегральных сумм. Определение П. последовательностей обобщается на случай направленных (частично упорядоченных) множеств.

Предел функции (отображения). Пусть Xи Y - топологич. пространства, Е X, х ₀ - точка прикосновения множества E, f : Е Y - отображение Ев Y. Точку наз. пределом отображения f в точке х ₀ (или, как говорят, при х, стремящемся к х ₀).и пишут

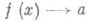или при ,

если, какова бы ни была окрестность V=V(a).точки а в Y, существует такая окрестность U=U(x₀).точки х ₀ в X, что для любой точки ее образ f(х).принадлежит . Иначе говоря, если Если Y - хаусдорфово пространство, то отображение

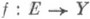может иметь только один П. в точке 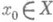. В случае, когда и х ₀ - точка прикосновения множества Е*, то П. сужения f_E* отображения f на множестве Е* наз. П. отображения (функции) f по множеству Е*, при этом пишут

Если 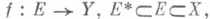х ₀- точка прикосновения множества Е* к существует 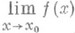, то в точке х ₀ существует и предел f по множеству Е*, причем

Если и существуют

то существует и

При рассмотрении П. отображения (функции) f : Е Y, ЕX, при может случиться, что или, наоборот, 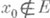. Случай представляет специальный интерес, т. к. он приводит к понятию непрерывной функции: если и , то для того, чтобы отображение f имело П. в точке х ₀, необходимо и достаточно, чтобы

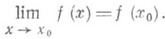
В случае выполнения этого условия отображение f и наз. непрерывным в точке х ₀. Если точка x₀ является изолированной точкой множества Е, то в ней всегда существует предел

для любого отображения f : Е Y, т. о. любое отображение f непрерывно во всех изолированных точках множества своего определения. Поэтому понятие П. отображения, в частности его непрерывности, содержательно лишь для предельных точек отображаемого множества. В классич. случае П. функций f : Е 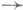Y обычно предполагается, что , т. <е. что точка х ₀ не принадлежит тому множеству, по к-рому берется П.

Если в точке для пространства Xвыполняется первая аксиома счетности, а пространство Y - хаусдорфово, то для того, чтобы существовал предел отображения , необходимо и достаточно, чтобы для лк бой последовательности , n = 1, 2, ... ,, существовал предел . При выполнении этого условия предел не зависит от выбора указанной последовательности {х _п} и их общее значение является П. отображения f в точке х ₀.

Предел последовательности точек {y_n} топологич. пространства Yявляется частным случаем П. отображения (функции): в этом случае Е= - множество натуральных чисел, рассматриваемых с дискретной топологией, 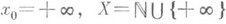, окрестностью в X является любое подмножество вида , где n₀ - нек-рое натуральное число.

Понятие предела кратной последовательности, т. е. последовательности, члены к-рой снабжены целочисленными мультииндексами, также является частным случаем П. отображения.

Внутренний критерий существования П. отображения f : Е Y в данной точке х ₀ (он наз. критерием Коши) в случае, когда в точке х ₀ топологич. пространства выполняется первая аксиома счетности, а множество Y является полным метрич. пространством, состоит в том, что предел существует тогда и только тогда, когда для любого 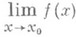e>0 найдется такая окрестность U=U( х ₀).точки х ₀ в X, что для всех точек х' и х ", удовлетворяющих условию , выполняется неравенство . В частности, этот критерий справедлив, когда Yявляется множеством действительных или комплексных чисел.

Некоторые свойства пределов. Если Y - метрич. пространство, , и существует предел , то найдется такая окрестность U=U(x₀). точки х ₀, что при отображении f образ пересечения 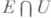отображаемого множества Ес этой окрестностью будет ограниченным подмножеством пространства Y.

Если функция -множество действительных чисел, имеет в точке не равный нулю конечный П., то существуют такие окрестность U=U(x₀). точки х ₀ и число с>0, что для всех точек выполняются неравенства f(х).> с, если f(х).< - с, если

Если Y - топологич. группа (в частности, коммутативная с аддитивной записью групповой операции), 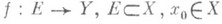, то предел существует тогда и только тогда, когда функция a(x)=-f(x)a^-1 имеет в точке x₀ предел, равный единице группы Y (соответственно функция a(x)=f(x) -а имеет П. в х _a, равный нулю,- такие функции наз. бесконечно малыми функциями).

Если Y - линейное топологич. пространство над полем то П. в точке x₀ линейной комбинации отображений f₁ и f₂ равен такой же линейной комбинации их П. в той же точке:

Если Y - множество действительных или комплексных чисел, (такие функции наз. числовыми), , то

а если , то

причем в этом случае под понимается П. сужения функции на пересечение отображаемого множества Ес нек-рой окрестностью точки х ₀ такой, что на указанном пересечении имеет смысл частное . Если , и существуют пределы ,

, то .

Если Xи Yполучены из множества действительных чисел пополнением его либо бесконечностью без знака: , либо двумя бесконечностями со знаком:

, то сформулированное определение П. функции является классич. определением конечного и бесконечного П. действительной функции одного переменного. Аналогично, если пространства Xи Yполучаются пополнением бесконечностью множества комплексных чисел , то получают определение П. (конечного и бесконечного) для функций комплексного переменного. Если же пространство X получается пополнением бесконечностью пространства (соответственно ), n>1, то получают определение конечного и бесконечного П. функции многих переменных при стремлении аргумента к конечной или бесконечно удаленной точке.

Для функций, определенных на подмножествах числовой прямой (или, более общо, на упорядоченных множествах), существует понятие одностороннего предела. Примером функций, имеющих по крайней мере один односторонний П. во всех предельных точках области определения, являются действительные монотонные функции: если функция f монотонна на множестве Ечисловой оси и точка x₀ является предельной точкой множества Е, то она является и предельной точкой хотя бы одного из множеств Е ₁=Е{: x<а}, Е ₂=Е{: х>а}. Если точка х ₀ предельная для множества E₁ то у функции f в точке х ₀ существует П. слева, а если она предельная для Е ₂, то справа. При этом если, напр., функция f возрастает и ограничена сверху, , х ₀ - предельная точка для множества E₁, то предел конечен.

Основным общим 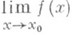методом отыскания П. функций является метод выделения главных частей функций в окрестности данной точки, что обычно делается с помощью Тейлора формулы. Для вычисления П. часто бывает полезно Лопиталя правило.

Несмотря на большую общность понятия П. отображения, оно не охватывает все существующие понятия П., имеющиеся в современной математике. Напр., понятие П. интегральных сумм не содержится в понятии

П. отображения (функции). Достаточно общим понятием П., в определенном смысле охватывающим все основные случаи, является П. отображения по фильтру.

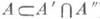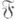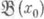Предел фильтра. Пусть X - топологии, пространство, - его база топологии, - фильтр на X(т. е. такое непустое семейство непустых подмножеств пространства X, что для любых существует такое , что ). Точка х ₀ наз. пределом фильтра или его .предельной точкой, если фильтр сильнее фильтра , являющегося локальной базой топологии в точке х ₀, т. е. для любого существует такое , что

Пусть - множество натуральных чисел с дискретной топологией. Фильтр на множестве , состоящий из всевозможных дополнений к конечным подмножествам множества , наз. натуральным фильтром и обозначается . Он не имеет П. в . Тот же фильтр на множестве 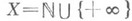, в к-ром локальная база состоит из всевозможных множеств , а при 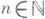- из одной точки n, имеет своим П. бесконечность . Единственность П. фильтра топологич. пространства связана с отделимостью точек пространства: для того чтобы любой фильтр топологич. пространства имел не более одного П., необходимо и достаточно, чтобы пространство было хаусдорфово.

Пусть X - нек-рое множество, Y - топологич. пространство, j - отображение Xв Y, 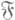- фильтр на X. Точку наз. пределом отображения Ф по фильтру 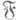и пишут

если фильтр , состоящий из всевозможных множеств Х, имеет своим П. в пространстве Yточку b.

Если Х~ - множество натуральных чисел, j - отображение в топологич. пространство Y,j(n)= - натуральный фильтр, то П. отображения ф по фильтру в пространстве Yсовпадает с обычным П. последовательности {у _п} в Y.

Если в - фильтр на X, являющийся произведением двух натуральных фильтров 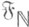, т. е. состоящий из всевозможных множеств вида 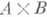, где - отображение в топологич. пространство , то П. отображения j по фильтру в пространстве Y совпадает с обычным П. двойной последовательности {у _пт} в Y. Пусть элементами множества Xявляются, в свою очередь, множества х, состоящие из какого-либо разбиения нек-рого отрезка [ а, b]; a=t₀<t₁<...<t_n-1<t_n=b и каких-то точек 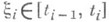, i=1,2,... , то есть

х = {t,x₁,..., x_n).

Пусть А _h (для любого h>0) - подмножество множества X, состоящее из всех элементов , у к-рых мелкости входящих в них разбиений 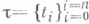меньше h, то есть

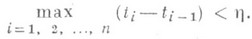
Система является фильтром. Всякая действительная функция f, определенная на отрезке [ а, b], порождает отображение j_f множества Xв числовую ось по формуле

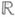Таким образом, j_f (х). является значением интегральной суммы Римана функции f, соответствующим элементу П. отображения j_f в по фильтру совпадает с обычным П. интегральных сумм Римана функции fпри условии, что мелкости рассматриваемых разбиений стремятся к нулю. Это совпадение имеет место в том смысле, что оба П. одновременно существуют или нет, а если существуют, то равны и являются значениями интеграла Римана от функции f по отрезку [ а, b].

Предел отображения топологических пространств по фильтру. Пусть Xи Y - топологич. пространства, 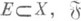- фильтр на E, j - отображение Ев Y. Точку наз. пределом отображения j в точке 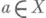по фильтру , если о является П. фильтра 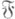, а bявляется П. фильтра . В этом случае пишут ,

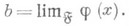
Если - база окрестностей в точке а, Е=Х{а}, а фильтр 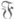состоит из всевозможных "проколотых окрестностей" U(а){а} точки , то предел 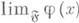совпадает с обычным пределом 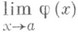отображения ф в точке а, то есть обобщает классическое определение П. отображения, сформулированное в терминах окрестностей. Непосредственным обобщением понятия П. последовательности является П. направленного множества в топологическом пространстве, т. е. такого частично упорядоченного множества, у к-рого за каждыми двумя элементами имеется следующий. В терминах П. по направленным множествам можно также сформулировать понятие П. отображения одного топологич. пространства в другое (см. Направленность, Сходимость).

Предел последовательности множеств. Топологический предел. Пусть А _п, п=1, 2, ... ,- множества топологич. пространства X. Верхним топологическим пределом последовательности {А _n} наз. множество точек , каждая окрестность к-рых пересекается с бесконечным числом множеств А _п, а нижним топологическим пределом 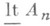- множество точек, каждая окрестность к-рых содержит точки почти всех А _п. Очевидно, . Если А , то последовательность {А _п} наз. сходящейся, а множество Аее топологическим П. и пишут A = It А _п. Верхний и нижний топологические П. последовательности являются замкнутыми множествами.

Теоретико-множественный предел. Имеется понятие П. последовательности множеств, не связанное с топологией. Последовательность множеств А _п, n=1, 2, ... , наз. сходящейся, если существует такое множество А, называемое ее пределом и обозначаемое

А=liт А _n,

что каждая его точка принадлежит всем множествам А _п, начиная с нек-рого номера, и каждая точка из объединения всех множеств А _п, не принадлежащая А, содержится лишь в конечном числе множеств А _п. Множество Аявляется П. последовательности { А _п}тогда и только тогда, когда оно является одновременно ее верхним и нижним пределом.

Лит.:[1] Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971; [2] Ильин В. А., Садовничий В. А., Сендов Б. X., Математический анализ, М., 1979; [3] Кудрявцев Л. Д., Курс математического анализа, т. 1-2, М., 1981; [4] Никольский С. М., Курс математического анализа, 2 изд., т. 1, М., 1975; 15] Бурбаки Н., Общая топологи". Основные структуры, пер.

о франц., 2 изд., М., 1958; [6] Замайский М., Введение в современную алгебру и анализ, пер. с франц., М., 1974; Е7] Келли Д ж. Д., Общая топология, пер. с англ., 2 изд., М., 1981; t8] X а у с д о р ф Ф., Теория множеств, пер. с нем., М.-Л., 1937. Л. <Д. <Кудрявцев.