ПОЛЯРИТЕТ

, полярное преобразование,- корреляцияp, для к-рой p²=id, то есть p(Y) =Xтогда и только тогда, когда p(X)=Y. П. разбивает все подпространства на пары, в частности, если пара образована подпространствами S₀ и S_n-1, где S₀=n(S_n-1) - точка, а S_n-1=p(S₀) -гиперплоскость, то S₀ наз. полюсом гиперплоскости S_n-1, a S_n-1 наз. полярой точки S₀. Пространство П _п (К).над телом Кобладает П. тогда и только тогда, когда тело допускает инволютивный инверсный автоморфизм a (т. е. a²=id). Пусть p представляется полубилинейной формой f_a(x, у). Тогда p будет П. в том и только в том случае, когда из f_a( х, y) = 0 следует f_a(y, x) = 0.

Поляритет p является либо симплектической корреляцией, характеризующейся тем, что для любой точки Р(в этом случае f ( х, у).является кососимметрич. формой на A_n+1, а К - полем), либо p представляется a-симметрич. формой на А _n+1:a(f_a(x,y))=f_a(y,x). (симметрический П.), в этом случае существование нестрого изотропного нулевого подпространства равносильно тому, что характеристика тела саг К=2 (в частности, если Саг К 2, то любое нулевое подпространство строго изотропно).

Относительно поляритета p определяется разложение проективного пространства на подпространства, позволяющее привести полубилинейную форму, представляющую p, к канонич. виду. Важнейшими среди них являются:

М - максимальное неизотропное нулевое подпространство, его размерность n(p)-1, где пчетно и наз. дефектом p, f кососимметрична;

U- максимальное строго изотропное нулевое подпространство, его размерность i(p)- 1, iназ. индексом, ;

J- компонента, свободная от нулевых подпространств, неизотропна, причем f является положительно или отрицательно определенной, ;

W=M+U - максимальное нулевое подпространство, его размерность i(p)+n(p)-1.

Проективное преобразование Fназ. p-допустимым (относительно поляритета p), если pF=Fp. Полулинейное преобразование тогда и только тогда индуцирует p-допустимое проективное преобразование, когда в K существует стакое, что 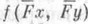=cj(f(x,y)).p-допустимые преобразования образуют группу С _p (наз. группой П.). Если группа G_p транзитивна, то либо каждая точка пространства ПД является нулевой (и С _p в этом случае наз. симплектической), либо нет ни одной нулевой точки (и G_p наз. в этом случае ортогональной при a=id и унитарной при ).

Лит.:[1] Ефимов Н. В., Высшая геометрия, 6 изд., М., 1978. М. И. Войцеховский.