Полупрямое произведение — Полупрямое произведение конструкция в теории групп, позволяющая строить новую группу по двум группам и , и действию группы на группе автоморфизмами. Полупрямое произведение групп и над … Википедия
Прямое произведение — Прямое или декартово произведение множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих… … Википедия
Декартово произведение — Прямое или декартово произведение множеств множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих … Википедия
Декартово произведение групп — Прямое или декартово произведение множеств множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих … Википедия
Декартово произведение множеств — Прямое или декартово произведение множеств множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих … Википедия
Прямое произведение графов — Прямое или декартово произведение множеств множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих … Википедия
Прямое произведение групп — Прямое или декартово произведение множеств множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих … Википедия
Прямое произведение множеств — Прямое или декартово произведение множеств множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих … Википедия
КОРНЕВАЯ СИСТЕМА — конечное множество Л векторов векторного пространства Vнад полем R, обладающее следующими свойствами: 1) Rне содержит нулевого вектора и порождает V;2) для каждого существует такой элемент а* сопряженного к F пространства V*, что и что… … Математическая энциклопедия
Декартова степень — Прямое или декартово произведение множеств множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих … Википедия
={1}. Если также и Анормальна в G, то П. п. превращается в прямое произведение. П. п. по группам Аи В строится неоднозначно. Для построения П. п. нужно еще знать, какие автоморфизмы на группе Ввызывают сопряжения элементами из А . Точнее, если G=AB - П. п., то каждому элементу 
соответствует автоморфизм 
, являющийся сопряжением элементом а:
есть гомоморфизм А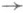 
Aut В. Обратно, если Аи В - произвольные группы, то для любого гомоморфизма 
существует единственное П. п. группы Ана группу Втакое, что aa=j(а) для любого 
. П. п. является частным случаем расширения группы Вс помощью группы А, такое расширение наз. расщепляющимся.