БЕРНУЛЛИ БЛУЖДАНИЕ

- случайное блуждание, порождаемое Бернулли испытаниями. На примере Б. б. можно пояснить нек-рые основные черты более общих случайных блужданий. В частности, уже в этой простейшей схеме проявляются свойства "случайности", парадоксальные с точки зрения интуиции.

Б. б. можно описать, напр., в следующих терминах. Частица движется по оси х("блуждает") по решетке точек вида . Движение начинается в момент , и положение частицы отмечается только в дискретные моменты времени На каждом шаге координата частица увеличивается или уменьшается на величину hс вероятностями ри соответственно, независимо от

предшествующего движения. Таким образом, перемещения в положительном и отрицательном направлениях ("успехи" и "неудачи") описываются схемой испытаний Бернулли с вероятностью успеха, равной р. Обычно Б. б. изображают геометрически, беря ось t за ось абсцисс, а ось х - за ось ординат (см. рис. 1; где показан начальный участок графика движения частицы, начинающей блуждание из нуля). Пусть - случайная величина, равная перемещению частицы на j- м шаге. Тогда образуют последовательность независимых случайных величин. 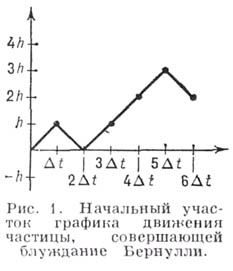Координата блуждающей частицы в момент равна сумме 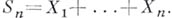Поэтому график Б. б. дает также наглядное представление о поведении нарастающих сумм случайных величин, причем многие характерные черты флуктуаций сохраняются и для сумм значительно более общих случайных величин. Этот график показывает также изменения капитала одного из игроков в классич. задаче о разорении (именно в связи с этой задачей были найдены формулы для вероятностей многих событий в Б. б.).

В физике Б. б. используют для грубого описания одномерных процессов диффузии (см. Диффузионный процесс).и броуновского движения материальных частиц под действием ударов молекул.

Из важнейших фактов, связанных с Б. б., можно отметить следующие (при этом ниже, если не оговорено противное, принято допущение ).

Вероятности возвращения. Пусть блуждание начинается из нуля. Тогда вероятность хотя бы одного возвращения в нуль равна 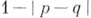, т. е. равна единице в симметричном случае 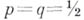и меньше единицы при . В симметричном случае величины 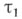(время до первого возвращения в нуль) и 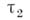(время между первым и вторым возвращениями) и т. д. суть независимые случайные величины с бесконечным математич. ожиданием. Время до -го возвращения, т. е. сумма растет как 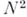, а среднее число N_2n возвращений за 2n шагов задается формулой

и растет как

Отсюда вытекает парадоксальное следствие: в симметричном Б. б. "волны" на графике между последовательными возвращениями в нуль оказываются поразительно длинными (рис. 2). С этим связано и другое обстоятельство, а именно, что для (доли времени, когда график находится выше оси абсцисс) наименее вероятными оказываются значения, близкие к 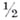Точнее, справедливо следующее утверждение: при 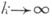, для вероятности равенства имеет место формула: где . Следствием является так наз. закон арксинуса: при каждом вероятность неравенства 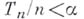стремится к

Опираясь на этот факт, можно показать, что при 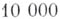шагов частица остается на положительной стороне более чем моментов времени с вероятностью т. е., грубо говоря, подобное положение будет наблюдаться не реже, чем в одном случае из десяти (хотя на первый взгляд оно кажется абсурдным).

Максимальное отклонение. При или блуждающая частица уходит с вероятностью единица в или . Поэтому, напр., при определена случайная величина

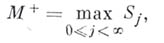
и вероятность того, что , равна

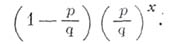
Бернулли блуждание с границами. Часто рассматривают Б. б. при наличии поглощающих пли отражающих экранов. Пусть, напр., блуждание начинается из нуля. Наличие в точке апоглощающего экрана проявляется в том, что по достижении этой точки частица перестает двигаться. При наличии в точке отражающего экрана частица с вероятностью qпереходит из и с вероятностью ростается на месте. Основным средством вычисления вероятностей поглощения и вероятностей достижения тех или иных точек служат развостные ¹ уравнения. Пусть, напр., поглощающий экран стоит в точке . Если 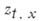есть вероятность того, что частица, находящаяся в точке 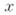в момент времени , поглотится до момента (включительно), то имеет место уравнение:

со следующими очевидными граничными условиями:

Решение этой задачи при было известно А. Муавру (A.'Moivre) и П. Лапласу (P. Laplace). Формула Лапласа имеет вид:

Переход к процессам диффузии. Пусть, напр., Тогда при многие вероятности, вычисленные для схемы Б. б.,

стремятся к пределам, равным аналогичным вероятностям для броуновского движения. Пусть речь .идет о вероятности того, что частица, вышедшая из нуля, поглотится экраном, стоящим в точке , до момента Предельным переходом из формулы (*) при , 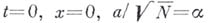получается величина

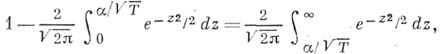
равная вероятности того, что координата 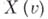частицы, совершающей броуновское движение, удовлетворяет неравенству: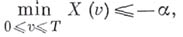

т. е. вероятности того, что частица поглотится на барьере - 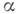. Для более или менее полного описания всех подобных предельных соотношений уместно встать на общую точку зрения и рассмотреть переход от дискретного процесса "нарастающих сумм" к непрерывному случайному процессу (см.. Предельные теоремы).

На схеме Б. б. можно весьма наглядно пояснить такие закономерности поведения сумм случайных величин, как больших чисел усиленный закон и повторного логарифма закон.

Лит.:[1] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 1-2, М-, 1967.

Ю. В. Прохоров.