МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ

среднее значение, случайной величины - числовая характеристика распределения вероятностей случайной величины. Самым общим образом М. о. случайной величины Х(w),определяется как интеграл Лебега по отношению к вероятностной мере в исходном вероятностном пространстве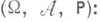

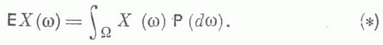
М. о. может быть вычислено и как интеграл Лебега от хпо распределению вероятностей Р _Х величины X:

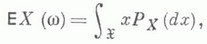
где 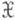- множество всех возможных значений X. М. о. функций от случайной величины Xвыражается через распределение Р _Х:напр., если X - случайная величина со значениями в 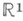и f(x) - однозначная бо-релевская функция х, то

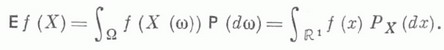
Если F(x) - функция распределения X, то М. о. представимо интегралом Лебега - Стилтьеса (или Римана - Стилтьеса)

при этом интегрируемость Xв смысле (*) равносильна конечности интеграла

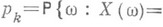
В частных случаях, если Xимеет дискретное распределение с возможными значениями х _k, k=1, 2, . . ., и соответствующими вероятностями 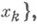то

если Xимеет абсолютно непрерывное распределение с плотностью вероятности р(х), то

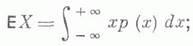
при этом существование М. о. равносильно абсолютной сходимости соответствующего ряда или интеграла. Основные свойства М. о.:

а)

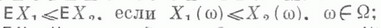
б) ЕС=С для любого действительного С:

в)

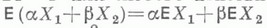
для любых действительных a и b;

г)

если сходится ряд

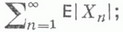
д) 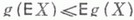для выпуклых функции g(x).

е) любая ограниченная случайная величина имеет конечное М. о. Кроме того,

ж)

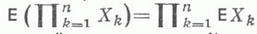
для взаимно независимых случайных величин X₁, ..., Х _п.

Естественным образом можно определить понятие случайной величины с бесконечным М. о. Типичным примером служат времена возвращения в нек-рых случайных блужданиях (см., напр., Бернулли блуждание).

С помощью М. о. определяются многие числовые и функциональные характеристики распределения (как М. о. соответствующих функций от случайной величины), напр, производящая функция, характеристическая функция, моменты любого порядка, в частности дисперсия, ковариация.

М. о. есть характеристика расположения значений случайной величины (среднее значение ее распределения). В этом качестве М. о. служит нек-рым "типичным" параметром распределения и его роль аналогична роли статич. момента - координаты центра тяжести распределения массы - в механике. От прочих характеристик расположения, с помощью к-рых распределение описывается в общих чертах,- медиан, мод, М. о. отличается тем большим значением, к-рое оно и соответствующая ему характеристика рассеяния - дисперсия - имеют в предельных теоремах теории вероятностей. С наибольшей полнотой смысл М. о. раскрывается больших чисел законом (см. также Чебышева неравенство )и больших чисел усиленным законом. В частности, для последовательности взаимно независимых и одинаково распределенных случайных величин 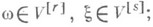с конечными М. о.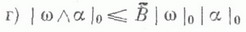при для любого

и, более того,

с вероятностью единица.

Понятие М. о. как ожидаемого значения случайной величины впервые наметилось в 18 в. в связи с теорией азартных игр. Первоначально термин "М. о." был введен как ожидаемый выигрыш игрока, равный для возможных выигрышей и соответствующих вероятностей Особые заслуги в обобщении и использовании понятия М. о. в современном его значении имеет П. Л. Чебышев.

Лит.:[1] Колмогоров А. Н., Основные понятия теории вероятностей, 2 изд., М., 1974; [2] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., тт. 1-2, М., 1967; [3] Лоэв М., Теория вероятностей, пер. с англ., М., 1962; [4] Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975. А. В. Прохоров.