- ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
экспоненциальная функция, экспонента,- функция
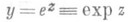
(где е- основание натуральных логарифмов- ненерово число), для любого значения z (действительного или комплексного) определяемая соотношением
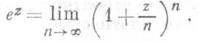 (1)
(1) Она обладает следующими свойствами:

при любых значениях z1 и z2.
При действительных хграфик П. ф. у=е х- експоненциальная кривая - проходит через точку (0, 1) и асимптотически приближается к оси Ох (см. рис.).
В курсе математич. анализа рассматривается П. ф. у = а х при действительных хи a>0,
 ; она связана с (основной) П. ф. у=е х соотношением
; она связана с (основной) П. ф. у=е х соотношением

П. ф. у-а х определена при всех х, положительна, монотонна (возрастает, если а>1, и убывает, если 0<а<1), непрерывна, бесконечно дифференцируема; при этом

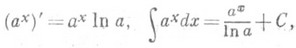
в частности

в окрестности каждой точки П. ф. может быть разложена в степенной ряд, напр.:
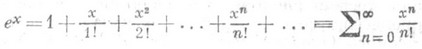 (2)
(2)
График П. ф. у=а х симметричен графику П. ф. y=(1/a)x относительно оси ординат. Если a>1, то П. ф. а х при
 возрастает быстрее любой степени х, а при
возрастает быстрее любой степени х, а при  стремится к нулю быстрее любой степени 1/х, т. е. при любом натуральном b>0
стремится к нулю быстрее любой степени 1/х, т. е. при любом натуральном b>0
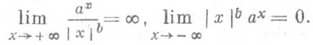
Обратной к П. ф. является логарифмическая функция.
При комплексных a и z П. ф. связана с (основной) П. ф. w=ez формулой
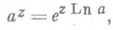
где Ln a - логарифм комплексного числа а.
П. ф. w=е z- целая трансцендентная функция и является аналитич. родолжением П. ф. у=е х с действительной оси в комплексную плоскость.
Помимо формулы (1), П. ф. может быть определена также с помощью ряда (2), сходящегося во всей комплексной плоскости, или по формуле Эйлера

если z= x+iy, ТО
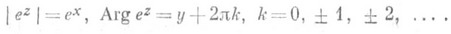
П. ф. ez- периодическая с периодом 2pi:
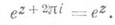
П. ф. е z принимает все комплексные значения, за исключением нуля: уравнение ez=a имеет бесконечное число решений для любого комплексного числа
 Эти решения находятся по формуле
Эти решения находятся по формуле

П. ф. ez является одной из основных элементарных функций. Через нее выражаются, напр., тригонометрич. функции и гиперболич. функции. Ю. В. Сидоров.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
