- ПОВТОРНОГО ЛОГАРИФМА ЗАКОН
предельная теорема теории вероятностей, являющаяся уточнением больших чисел усиленного закона. Пусть X1, Х 2, . . .- последовательность случайных величин и
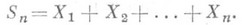
Для простоты предполагается, что Sn для каждого пимеет нуль своей медианой. В то время как теоремы об усиленном законе больших чисел указывают условия, при к-рых
почти наверное (п. н.) при 
, где {а п} - числовая последовательность, теоремы о П. л. з. имеют дело с числовыми последовательностями {с n} такими, что
п. <н. (1)
или
п. <п. (2)
Соотношение (1) равносильно тому, что
и 
для любого e>0, где запись "б. ч." означает бесконечное число раз.
Соотношения вида (1) и (2) справедливы при более ограничительных условиях, чем оценки, вытекающие из усиленного закона больших чисел. Если {Х n} - последовательность независимых случайных величин, имеющих одинаковое распределение с математич. ожиданием, равным нулю, то
п. <н. при 
(теорема Колмогорова); если выполнено дополнительное условие 
, то имеет место более сильное соотношение (2), в к-ром
где
(теорема Хартмана - Винтнера).
Первой теоремой общего типа о законе повторного логарифма был следующий результат А. Н. Колмогорова [1]. Пусть {Х п}- последовательность независимых случайных величин с математич. ожиданиями, равными нулю, конечными дисперсиями и пусть
Если
при 
и существует последовательность положительных постоянных {М n} такая, что
то выполнены соотношения (1) и (2) при
В частном случае, когда {Х п} - последовательность независимых случайных величин, имеющих одинаковое распределение с двумя значениями, это утверждение было получено А. Я. Хинчиным [2]. IO. Марцинкевич и А. Зигмунд [3] показали, что в условиях теоремы Колмогорова нельзя заменить о на О. Обобщения П. л. з. Колмогорова для последовательностей независимых ограниченных неодинаково распределенных случайных величин были исследованы В. Феллером [4]. Другие обобщения П. л. з. см. в [5]; имеется также следующий результат (см. [6]), примыкающий к теореме Хартмана - Винтнера: если {Х п} - последовательность независимых случайных величин, имеющих одинаковое распределение с бесконечной дисперсией, то
п. <н.
Результаты, полученные в области П. л. з. для последовательностей независимых случайных величин, послужили отправным пунктом для многочисленных исследований применимости П. л. з. к последовательностям зависимых случайных величин и векторов и к случайным процессам.
Лит.:[1] Колмогоров А. Н., "Math. Ann.", 1929, Bd 101, S. 126-35; [2] Xинчин А. Я., "Fundam. math.", 1924, v. 6, p. 9-20; [3] Marcinkiewicz J., Zygmund A., там же, 1937, v. 29, p. 215-22; [4] Feller W., "Trails. Amer. Math. Soc.", 1943, v. 54, p. 373-402; [5] Strassen V., "Z. Wahrscheinlichkeitstheor. und verw. Geb.", 1964, Bd 3, S. 211-26; [6] его же, там же, 1965-66, Bd 4, S. 265-68' [7] Наrtman P., Wintnеr A., "Amer. J. Math.", 1941, v. 63, p. 169- 176; 18] Ламперти Д ж., Вероятность, пер. сангл., М., 1973; [9] Петров В. В., Суммы независимых случайных величин, М., 1972. В. В. Петров.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
