ПЛОТНОСТНАЯ ГИПОТЕЗА

предполагаемое неравенство, доставляющее оценку для числа N(s, Т).нулей r=b+ig дзета-функции Римана

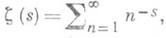
где s=s+it, в прямоугольнике

Наиболее точная формулировка П. г.:

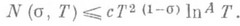
Более простой, но менее точный вид П. г.:

П. г. позволяет получать в теории простых чисел результаты, сравнимые с теми, к-рые вытекают из гипотезы Римана. Напр., из П. г. следует, что при достаточно больших хв каждом сегменте содержится хотя бы одно простое число.

П. г. является следствием более сильной Линделёфа гипотезы. В отличие от последней П. г. частично доказана, т. к. содержится в плотностных теоремах, начиная с нек-рых значений

Для числа нулей L-функций Дирихле

где - характер по модулю k, имеет место аналогичная П. г. В усредненной форме она имеет вид

где 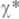- примитивный характер по модулю k.

П. г. для L-функций Дирихле применяется в теории распределения простых чисел, принадлежащих арифметич. прогрессиям.

Лит.:[1]Монтгомери Г., Мультипликативная теория чисел, пер. с англ., М., 1974; [2] Лаврик А. Ф., "Успехи матем. наук", 1980, т. 35, в. 2, с. 55-65. Б. М. Бредихин.