ГЛАДКИЙ МОРФИЗМ

ГЛАДКИЙ МОРФИЗМ

схем- обобщение на случай схем понятия семейства неособых алгебраических многообразий. В классич. случае морфизма комплексных алгебраич. многообразий это понятие сводится к понятию регулярного отображения (субмерсии) комплексных многообразий. Конечно представленный (локально) морфизм схем 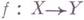наз. гладким морфизмом, если f есть плоский морфизм и если для любой точк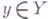и слой 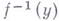будет гладкой схемой (над полем k(у)). Схема X наз. гладкой схемой над схемой Y, или гладкой Y-схемой, если структурный морфизм 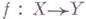является Г. м.

Примером гладкой Y-схемы служит аффинное пространство . Частный случай понятия Г. м. - этальный морфизм. Обратно, всякий Г. м. 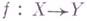разлагается локально по X в композицию этального морфизма и проекции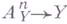

Композиция Г. м. снова есть Г. м.; аналогично обстоит дело с произвольной заменой базы. Г. м. характеризуется своим дифференциальным свойством: плоский конечно представленный морфизм 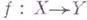будет Г. м. тогда и только тогда, когда пучок относительных дифференциалов есть локально свободный пучок ранга в точке х.

Понятие Г. м. аналогично понятию расслоения в смысле Серра в топологии. Напр., Г. м. комплексных алгебраич. многообразий является локально тривиальным дифференцируемым расслоением. В общем случае выполняется следующий аналог аксиомы о накрывающей гомотопии: для любой аффинной схемы Y', ее замкнутой подсхемы 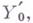определяемой нильпотентным идеалом, и любого морфизма канонич. отображение сюръективно.

Если 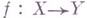есть Г. м., а локальное кольцоJY,y точки 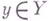является регулярным (соответственно нормальным, приведенным), то таким же будет и локальное кольцо JY,y любой точки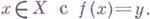

Лит.:[1] Grоthеndiесk A., "Publ. math. IHES", 1967, t. 32; [2] Revetements etales et groupe fondamental, В., (971. В. И. <Данилов, И. В. Долгачев.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем написать реферат

Полезное


Смотреть что такое "ГЛАДКИЙ МОРФИЗМ" в других словарях:

  • ЭТАЛЬНЫЙ МОРФИЗМ — гладкий морфизм алгебраич. многообразий или схем относительной размерности 0. Эквивалентным образом можно определить Э. м. схем как локально конечно представленный плоский морфизм такой, что для любой точки k(y) cxeмa конечна и сепарабельна. Э. м …   Математическая энциклопедия

  • ЛИНЕЙЧАТАЯ ПОВЕРХНОСТЬ — в дифференциальной геометрии поверхность, образованная движением прямой линии. Прямые, принадлежащие этой поверхности, называются прямолинейными образующими, а каждая кривая, пересекающая все прямолинейные образующие, направляющей кривой. Если… …   Математическая энциклопедия

  • ГЛАДКАЯ СХЕМА — обобщение понятия неособого алгебраического многообразия. Схема X(локально) конечного типа над полем kназ. гладкой схемой (над k), если схема, полученная из Xс помощью замены поля констант kна его алгебраяч. замыкание k, является регулярной… …   Математическая энциклопедия

  • МОДУЛЕЙ ТЕОРИЯ — теория, изучающая непрерывные семейства объектов алгебраич. геометрии. Пусть А класс объектов алгебраич. геометрии (многообразий, схем, векторных расслоений и т. п.), на к ром задано нек рое отношение эквивалентности R. Основная задача… …   Математическая энциклопедия

  • ПОЛЯРИЗОВАННОЕ АЛГЕБРАИЧЕСКОЕ МНОГООБРАЗИЕ — пара (V,x)> где V полное гладкое многообразие над алгебраически замкнутым полем k,| из Pic V/PicoV класс нек рого обильного обратимого пучка, PicoV связная компонента абелевой схемы Пикара Pic V. В случае, когда V абелево многообразие,… …   Математическая энциклопедия

  • РИМАНА - РОХА ТЕОРЕМА — теорема, позволяющая выразить эйлерову характеристику c(Е). локально свободного пучка Ена алгебраическом или аналитич. многообразии Xв терминах характеристич. классов Чжэня пучка Еи многообразия X. Она может быть применена для вычисления… …   Математическая энциклопедия

  • ЭТАЛЬНЫЕ КОГОМОЛОГИИ — когомологии пучков в эталъной топологии. Они определяются стандартным образом при помощи производных функторов. А именно, пусть X схема и Xet этальная топология на X. Тогда категория пучков абелевых групп на Xet является абелевой категорией с… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»