ПЕТЕРСОНА - КОДАЦЦИ УРАВНЕНИЯ
- ПЕТЕРСОНА - КОДАЦЦИ УРАВНЕНИЯ
уравнения, составляющие вместе с уравнением Гаусса (см. Гаусса теорема).необходимые и достаточные условия интегрируемости системы, к к-рой сводится задача восстановления поверхности по ее первой и второй квадратичным формам (см. Бонне теорема). П. - К. у. имеют вид
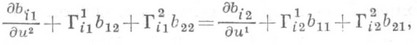
где bij- коэффициенты второй квадратичной формы, 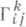 - символы Кристоффеля 2-го рода.
- символы Кристоффеля 2-го рода.
Уравнения впервые найдены К. М. Петерсоном в 1853, переоткрыты Г. Майнарди (G. Mainardi, 1856) и Д. Кодацци (D. Codazzi, 1867).
Лит.:[1] Рашевский П. К., Курс дифференциальной геометрии, М., 1956. А. Б. Иванов.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "ПЕТЕРСОНА - КОДАЦЦИ УРАВНЕНИЯ" в других словарях:
Уравнения Петерсона ― Кодацци — Уравнения Петерсона ― Майнарди ― Кодацци ― уравнения, составляющие вместе с уравнением Гаусса необходимые и достаточные условия интегрируемости системы, к которой сводится задача восстановления поверхности по её первой и второй квадратичным… … Википедия
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в к ром изучаются геометрич. образы, в первую очередь кривые и поверхности, методами математич. анализа. Обычно в Д. г. изучаются свойства кривых и поверхностей в малом, т. е. свойства сколь угодно малых их кусков. Кроме того, в … Математическая энциклопедия
Гиперповерхность — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Гиперповерх … Википедия
ПОГРУЖЕННЫХ МНОГООБРАЗИЙ ГЕОМЕТРИЯ — теория, изучающая внешнюю геометрию и связь между внешней и внутренней . геометрией подмногообразий евклидова или риманова пространства. П. м. г. является обобщением классич. дифференциальной геометрии поверхностей в евклидовом пространстве .… … Математическая энциклопедия
Петерсон, Карл Михайлович — В Википедии есть статьи о других людях с такой фамилией, см. Петерсон. Карл Михайлович Петерсон Kārlis Pētersons Дата рождения: 13 (25) мая 1828(1828 05 25) Место рождения … Википедия
ИЗОМЕТРИЧЕСКОЕ ПОГРУЖЕНИЕ — погружение k мерного метрич. многообразия М к в n мерное риманово пространство V, в виде k мерной поверхности Ф, при к ром расстояние между любыми двумя точками на М k совпадает с расстоянием между их образами, измеренным по поверхности Ф в… … Математическая энциклопедия
Уравнение синус-Гордона — Уравнение синус Гордона это нелинейное гиперболическое уравнение в частных производных в 1 + 1 измерениях, включающее в себя оператор Даламбера и синус неизвестной функции. Изначально оно было рассмотрено в XIX веке в связи с… … Википедия
ГАУССА ТЕОРЕМА — (theorema egregium): гауссова кривизна (произведение главных кривизн) регулярной поверхности в евклидовом пространстве не меняется при изгибаниях поверхности. (Здесь регулярность означает гладкое погружение.) Г. т. следует из того, что гауссова… … Математическая энциклопедия
КЛАСС — 1) Термин, употребляемый в математике в основном как синоним термина множество для обозначения произвольных совокупностей объектов, обладающих каким либо определенным свойством или признаком (напр., в алгебре классы эквивалентности относительно… … Математическая энциклопедия
РИЧЧИ ТОЖДЕСТВО — 1) Тождество, выражающее одно из свойств Римана тензора : Для ковариантного тензора тождество имеет вид т. е. циклирование по трем первым индексам дает нуль. 2) Тождество, к рому должны удовлетворять ковариантные производные 2 го порядка… … Математическая энциклопедия
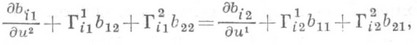
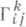 - символы Кристоффеля 2-го рода.
- символы Кристоффеля 2-го рода.