БЕЙЕСОВСКИЙ ПОДХОД ЭМПИРИЧЕСКИЙ

статистич. интерпретация бейесовского подхода к построению выводов о ненаблюдаемых значениях случайных параметров при неизвестном их априорном распределении. Пусть - случайный вектор, причем предполагается, что плотность условного распределения Yпри любом заданном значении случайного параметра известна. Если в результате нек-рого эксперимента наблюдается лишь реализация Y, а соответствующая реализация Xнеизвестна и требуется оценить значение заданной функции от ненаблюдаемой реализации, то согласно Б. п. э. в качестве приближенного значения следует использовать условное математич. ожидание Е{j(Х)|Y}, к-рое в силу Бейеса формулы выражается отношением

- плотность безусловного (априорного) распределения - соответствующая -конечная мера; функция представляет собой плотность безусловного распределения .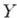

Если априорная плотность неизвестна, то вычисление значений невозможно. Однако, если имеется достаточно большое количество реализаций независимых случайных величин подчиняющихся распределению с плотностью то для можно построить состоятельную оценку зависящую лишь от Для оценки значения Бернштейн [1] предложил заменить в (2) и найти решение этого интегрального уравнения, а затем подставить в правую часть (1). Однако этот путь затруднителен, так как решение указанного интегрального уравнения принадлежит к числу некорректно поставленных задач вычислительной математики.

В нек-рых исключительных случаях статистич. подход может быть применен не только для оценки , но и (см. [3]). Такая возможность возникает тогда, когда справедливо тождество относительно

где - функции, зависящие лишь от у, а как функция от zявляется плотностью вероятности (т. е. ее можно рассматривать как плотность условного распределения нек-рой случайной величины при заданном значении ). Если (3) справедливо, то числитель отношения (1) равен произведению - плотность безусловного распределения Z. Т. о., если имеется достаточно большое количество реализаций независимых случайных величин подчиняющихся распределению с плотностью , то для можно построить состоятельную оценку , а значит, и найти состоятельную оценку для :

Напр., если требуется оценить , причем , то , где Так как здесь . Поэтому т. е. для отыскания нужна лишь последовательность реализаций Если же целое > 0 ; ), то , где и . Поэтому для построения в этом случае нужно иметь две последовательности эмпирических значений и .

Указанная методика Б. п. э. применима к весьма узкому классу плотностей и функций , удовлетворяющему условию (3); и если даже это условие выполняется, то для построения оценки (4) нужно располагать реализациями случайных величин , распределение к-рых, как правило, отлично от распределения непосредственно наблюдаемых величин . Для практич. целей предпочтительнее видоизмененная методика Б. п. э., лишенная указанных недостатков. Суть этого видоизменения заключается в построении не самой состоятельной оценки для (эта оценка может и не существовать), а нижней и верхней оценок для этой

функции, отыскание к-рых сводится к решению задачи линейного программирования следующим образом. Пусть - условные минимум и максимум линейного функционала (относительно неизвестной априорной плотности ) в числителе (1), вычисленные при линейных условиях и - упомянутая выше оценка для , построенная по результатам наблюдений ). В таком случае можно заключить, что , причем вероятность справедливости такого заключения в силу больших чисел закона стремится к единице при неограниченном увеличении количества случайных величин , используемых при построении оценки . Возможны и другие видоизменения Б. п. э., напр., за счет добавления к последнему условию конечного числа условий вида , где 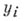- заранее заданные числа; если заменить соответствующими доверительными пределами для , то получаются условия в виде неравенств и т. д.

В нек-рых практически важных случаях для функций удается найти удовлетворительные мажоранты, вычисляемые без применения трудоемких методов линейного программирования (см. пример, посвященный статистич. контролю, в ст. Выборочный метод).

О применении Б. п. э. к решению задач статистич. проверки гипотез о значениях случайных параметров см. Дискриминантный анализ.

Лит.:Ш Бернштейн С. Н., "Изв. АН СССР. Сер. матем.", 1941, т. 5, с. 85-94; [2] Большее Л. Н., в кн.: Международный конгресс математиков в Ницце, 1970. Доклады советских математиков, М., 1972, с. 48-55; [31 Rоbbins H., в кн.: Proceedings Berkeley Symposium Mathematical Statistics and Probability, v. 1, Berk.-Los Ang., 1956, p. 157-63.

Л. Н. Большее.