ОСОБЫЕ ПОКАЗАТЕЛИ

линейной системы обыкновенных дифференциальных уравнений - величины, определяемые формулой:

(верхний особый показатель) или формулой

(нижний особый показатель), где - Коши оператор системы

где - отображение , суммируемое на каждом отрезке.

О. п. могут равняться ; если для нек-рого T>0

то О. п. суть числа.

Для системы (1) с постоянными коэффициентами О. п. и равны соответственно максимуму и минимуму действительных частей собственных значений оператора А(0). Для системы (1) с периодич. коэффициентами (A(t+T)=A(t).при всех для нек-рого Т>0).О. п. и равны соответственно максимуму и минимуму логарифмов модулей мультипликаторов, деленных на период Т. Иногда О. п. наз. иначе, напр. генеральными показателями (см. [4]).

Следующие определения эквивалентны приведенным выше: О. п. W⁰(A). равен точной нижней грани множества тех чисел а, для каждого из к-рых найдется число такое, что для всякого решения системы (1) выполнено неравенство

для всех

О. п. равен точной верхней грани множества тех чисел Р, для каждого из к-рых найдется число С _b >0 такое, что для всякого решения системы (1) выполнено неравенство

для всех

Для О. п. и Ляпунова характеристических, показателей имеют место неравенства:

Для линейных систем с постоянными или с периодич. коэффициентами

но существуют системы, для к-рых соответствующие неравенства - строгие (см. Равномерная устойчивость). О. п. (соответственно ) как функция на пространстве систем (1) с ограниченными непрерывными коэффициентами (отображение непрерывно и ), наделенном метрикой

полунепрерывна сверху (соответственно снизу), но не всюду непрерывна.

Если отображение равномерно непрерывно и

то сдвигов динамическая система имеет инвариантные нормированные меры m₁ и m₂, сосредоточенные на замыкании траектории точки А, такие, что для почти всех 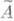(в смысле меры m₁).верхний О. п. системы

(2)

равен се наибольшему (старшему) характеристик, показателю Ляпунова

и для почти всех (в смысле меры m₂) нижний О, п. системы (2) равен ее наименьшему характеристич. показателю Ляпунова

Для почти периодич. отображения (см. Линейная система дифференциальных уравнений с почти периодическими коэффициентами).меры m₁ и m₂ идентичны и совпадают с той единственной нормированной инвариантной мерой, сосредоточенной на сужении динамич. системы сдвигов на замыкание траектории точки А, к-рая в этом случае имеется.

Пусть динамич. система на гладком замкнутом п- мерном многообразии Vⁿ задана гладким векторным полем. Тогда у этой системы найдутся нормированные инвариантные меры m₁ и m₂ такие, что для почти всякой (в смысле меры m₁) точки совпадают верхний О. п. и старший характеристич. показатель Ляпунова системы уравнений в вариациях вдоль траектории точки хи для почти всякой (в смысле меры m₂) точки совпадают нижний О. п. и наименьший характеристич. показатель Ляпунова системы уравнений в вариациях вдоль траектории точки х. Определения О. п., характеристич. показателей Ляпунова и т. п. сохраняют смысл для систем уравнений в вариациях гладких динамич. систем, заданных на любых гладких многообразиях. Система уравнений в вариациях такой динамич. системы вдоль траектории точки хможет быть записана в виде (1), напр. с помощью задания в касательном пространстве к Vⁿ в каждой точке траектории точки хбазиса, полученного параллельным перенесением вдоль траектории точки х(в смысле римановой связности, индуцированной какой-либо гладкой римановой метрикой) нек-рого базиса касательного пространства к Vⁿ в точке х.

Лит.:[1] Воhl P., "J. rcine und angew. Math.", 1913, Bd 144, S. 284-318; [2] Персидсиий К., "Матем. сб.", 1933, т. 40, № 3, с. 284-93; [3] Б ы л о в Б. Ф., В и н о г р а д Р. Э., Г р о б м а н Д. М., Н е м ы ц к и й В. В., Теория показателей Ляпунова и ее приложения к вопросам устойчивости, М., 196С; [4] Д а л е ц к и й Ю. Л., К р е й н М. Г., Устойчивость решений дифференциальных уравнений в банаховом пространстве, М., 1970; [5] Изобов Н. А., в кн.: Итоги науки и техники. Матем. анализ, т. 12, М., 1974, с. 71 -146. В. М. Миллионщиков.