БАРИЦЕНТРИЧЕСКИЕ КООРДИНАТЫ
- БАРИЦЕНТРИЧЕСКИЕ КООРДИНАТЫ
координаты точки n-мерного векторного пространства  , отнесенные к нек-рой фиксированной системе
, отнесенные к нек-рой фиксированной системе 
 точек, не лежащих в
точек, не лежащих в  -мерном подпространстве. Каждая точка
-мерном подпространстве. Каждая точка  может быть единственным образом представлена в виде
может быть единственным образом представлена в виде

где 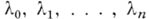 - действительные числа, удовлетворяющие условию
- действительные числа, удовлетворяющие условию  Точка х, по определению, есть центр тяжести масс
Точка х, по определению, есть центр тяжести масс  помещенных в точках
помещенных в точках  Числа
Числа  наз. барицентрическими координатам и точки х;точка с Б. к.
наз. барицентрическими координатам и точки х;точка с Б. к.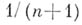 наз. барицентром.
наз. барицентром.
Б. к. введены А. Мёбиусом в 1827 (см. [1]) как ответ на вопрос о том, какие массы следует поместить в вершинах заданного треугольника, чтобы данная точка была центром тяжести этих масс. Б. к. являются частным случаем общих однородных координат;они аффинно инвариантны.
Б. к. точек симплекса используются в алгебраич. топологии (см. [2]). Барицентрическими координатами точек 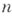 -мерного симплекса
-мерного симплекса  относительно его вершин
относительно его вершин 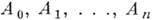 наз. их (общие) декартовы координаты в базисе векторов
наз. их (общие) декартовы координаты в базисе векторов 
 где
где 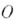 - любая точка, не лежащая в n-мер-ном подпространстве, несущем
- любая точка, не лежащая в n-мер-ном подпространстве, несущем  (считается, что
(считается, что  лежит в нек-ром евклидовом пространстве; при этом определение не зависит от точки
лежит в нек-ром евклидовом пространстве; при этом определение не зависит от точки  ), или проективные координаты относительно
), или проективные координаты относительно  в проективном пополнении содержащего а подпространства. Б. к. точек симплекса неотрицательны и их сумма равна единице. Обращение в нуль
в проективном пополнении содержащего а подпространства. Б. к. точек симплекса неотрицательны и их сумма равна единице. Обращение в нуль 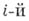 Б. к. равносильно тому, что точка лежит на противоположной вершине
Б. к. равносильно тому, что точка лежит на противоположной вершине 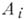 грани симплекса
грани симплекса  . Это позволяет рассматривать Б. к. точек геометрич. комплекса относительно всех его вершин. При помощи Б. к. производится барицентрическое подразделение комплекса.
. Это позволяет рассматривать Б. к. точек геометрич. комплекса относительно всех его вершин. При помощи Б. к. производится барицентрическое подразделение комплекса.
По аналогии с этим вводится формальное определение Б. к. для абстрактных симплексов (см. [3]).
Лит.:[1] Мobius A. P., Der barycentrische Calcul, в его кн.: Gesammelte Werke, Bd 1, Lpz., 1885; [2] Понтрягин Л. С., Основы комбинаторной топологии, 2 изд., М., 1976; [3] Спеньер Э., Алгебраическая топология, пер. с англ., М., 1971. Е. Г. Скляренко.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "БАРИЦЕНТРИЧЕСКИЕ КООРДИНАТЫ" в других словарях:
Барицентрические координаты — У этого термина существуют и другие значения, см. Координаты. Барицентрические координаты координаты точки мерного аффинного пространства , отнесенные к некоторой фиксированной системе из ой точки , не лежащих в мерном подпространстве.… … Википедия
барицентрические координаты — (см. барицентр) три числа, в сумме равные единице, определяющие положение точки в треугольнике, равные массам, которые следует поместить в вершинах треугольника так, чтобы определяемая точка сделалась центром тяжести этих масс. Новый словарь… … Словарь иностранных слов русского языка
Барицентрические координаты — точки М на плоскости по отношению к трём базисным (не лежащим на одной прямой) точкам A1, A2, А3 этой плоскости такие три числа m1, m2, m3 (связанные условием m1 + m2 +m3. = 1), что точка М представляет собой центр тяжести системы из трёх … Большая советская энциклопедия
Координаты — Координаты величины, определяющие положение точки (тела) в пространстве (на плоскости, на прямой). Совокупность координат всех точек пространства является системой координат. В Викисловаре есть статья «координата» Понятие и слово… … Википедия
КООРДИНАТЫ — числа, величины, по к рым находится (определяется) положение какого либо элемента (точки) в некоторой совокупности (множестве М), например на плоскости поверхности, в пространстве, на многообразии. В ряде разделов математики и физики К. именуются … Математическая энциклопедия
Трилинейные координаты — тесно связаны с барицентрическими координатами. А именно, если барицентрические координаты точки относительно треугольника , то её трилинейные координаты. Трилинейные координаты, как и барицентрические, определены с точностью до… … Википедия
Цилиндрические параболические координаты — Координатные поверхности в координатах параболического цилиндра. Цилиндрические параболические координаты (координаты параболи … Википедия
Параболические координаты — Параболические координаты ортогональная система координат на плоскости, в которой координатные линии являются конфокальными параболами. Трёхмерный вариант этой системы координат получается при вращении парабол вокруг их оси симметрии.… … Википедия
Биангулярные координаты — Биангулярные координаты система координат на плоскости с двумя фиксированными точками … Википедия
Биполярные координаты — Биполярная система координат … Википедия
 , отнесенные к нек-рой фиксированной системе
, отнесенные к нек-рой фиксированной системе 
 точек, не лежащих в
точек, не лежащих в  -мерном подпространстве. Каждая точка
-мерном подпространстве. Каждая точка  может быть единственным образом представлена в виде
может быть единственным образом представлена в виде 
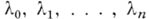 - действительные числа, удовлетворяющие условию
- действительные числа, удовлетворяющие условию  Точка х, по определению, есть центр тяжести масс
Точка х, по определению, есть центр тяжести масс  помещенных в точках
помещенных в точках  Числа
Числа  наз. барицентрическими координатам и точки х;точка с Б. к.
наз. барицентрическими координатам и точки х;точка с Б. к.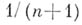 наз. барицентром.
наз. барицентром.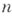 -мерного симплекса
-мерного симплекса  относительно его вершин
относительно его вершин 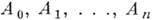 наз. их (общие) декартовы координаты в базисе векторов
наз. их (общие) декартовы координаты в базисе векторов 
 где
где 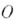 - любая точка, не лежащая в n-мер-ном подпространстве, несущем
- любая точка, не лежащая в n-мер-ном подпространстве, несущем  (считается, что
(считается, что  лежит в нек-ром евклидовом пространстве; при этом определение не зависит от точки
лежит в нек-ром евклидовом пространстве; при этом определение не зависит от точки  ), или проективные координаты относительно
), или проективные координаты относительно  в проективном пополнении содержащего а подпространства. Б. к. точек симплекса неотрицательны и их сумма равна единице. Обращение в нуль
в проективном пополнении содержащего а подпространства. Б. к. точек симплекса неотрицательны и их сумма равна единице. Обращение в нуль 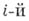 Б. к. равносильно тому, что точка лежит на противоположной вершине
Б. к. равносильно тому, что точка лежит на противоположной вершине 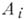 грани симплекса
грани симплекса  . Это позволяет рассматривать Б. к. точек геометрич. комплекса относительно всех его вершин. При помощи Б. к. производится барицентрическое подразделение комплекса.
. Это позволяет рассматривать Б. к. точек геометрич. комплекса относительно всех его вершин. При помощи Б. к. производится барицентрическое подразделение комплекса.