ОПЕРАТОРНАЯ ЭРГОДИЧЕСКАЯ ТЕОРЕМА

общее название теорем о пределе средних по неограниченно удлиняющемуся "промежутку времени" п=0, 1, . . .,N или для степеней {А ^п} линейного оператора А , действующего в банаховом (или даже топологическом векторном, см. [5]) пространстве Е, либо для действующей в Еоднопараметрич. полугруппы линейных операторов {At}. В последнем случае можно рассматривать также предел средних по неограниченно уменьшающемуся промежутку времени (локальные эргодические теоремы, см. [5], [6]; говорят также об "эргодичности в нуле", см. [1]). Средние могут пониматься в различных смыслах, аналогично тому, как это делается в теории суммирования рядов. Чаще всего используются средние Чезаро

или средние Абеля

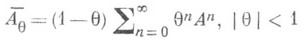
или

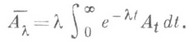
Условия эргодич. теорем заведомо обеспечивают сходимость подобных бесконечных рядов или интегралов; при этом, хотя абелевы средние образуются с участием всех А ⁿ или A_t, главную роль играют значения А ⁿ или A_t на конечном отрезке времени, неограниченно возрастающем при 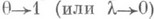. Предел средних и т. д.) тоже может пониматься в различных смыслах - в сильной или слабой операторной топологии (статистические эргодические теоремы, т. е. Неймана теорема эргодическая - исторически первая О. э. т.- и ее обобщения), в равномерной операторной топологии (равномерные эргодические теоремы, см. [1], [2], [3]), а если Ереализовано как нек-рое пространство функций на нек-ром пространстве с мерой, то и в смысле сходимости почти всюду средних и т. п. при (индивидуальные эргодические теоремы, т. е. Биркгофа эргодическая теорема и ее обобщения, см., напр., Орнстейна-Чекона эргодическая теорема;их, впрочем, не всегда относят к О. э. т.). Нек-рые из О. э. т. как бы сравнивают силу различных упомянутых выше вариантов, устанавливая, что из существования пределов средних в одном смысле следует существование пределов в другом смысле. В нек-рых теоремах речь идет не о пределе средних, а о пределе отношения двух средних (такова теорема Орнстейна - Чекона).

Имеются также О. э. т. для n-параметрических и даже более общих полугрупп.

Лит.:[1] Xилле Э., Филлипс Р., Функциональный анализ и полугруппы, пер. с англ., М., 1962; [2] Данфорд Н., Шварц Дж., Линейные операторы. Общая теория, пер. с англ., М., 1962; [3] Неве Ж., Математические основы теории вероятностей, пер. с франц., М., 1969; [4] В е р ш и к А. М., Ю з в и н-с к и и С. А., в кн.: Итоги науки, в. 15 - Математический анализ. 1967, М., 1969, с. 133-87; [5] Каток А. Б., Синай Я. Г., С т е п и н А. М., в кн.: Итоги науки и техники. Сер. Математический анализ, т. 13, М., 1975, с. 129-262; [Ц] КrеngеI U., "Asterisque", 1977, t. 50, p. 151-'92. Д. В. Аносоа.