ОМЕГА-НЕПРОТИВОРЕЧИВОСТЬ

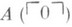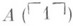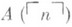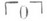свойство формальных арифметич. систем, означающее невозможность получения омега-противоречия. Омега-противоречием наз. такая ситуация, когда для некрой формулы (х).доказуема каждая формула из бесконечной последовательности формул , , . . ., , . . . и формула , где - константа формальной системы, обозначающая число 0 а константы 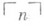определяются рекурсивно через терм (х)., обозначающий число, непосредственно следующее

за х:

Понятие О.-н. появилось в связи с Гёделя теоремой о неполноте арифметики. Именно в предположении О.-н. формальной арифметики К. Гёдель (К. Godel) доказал ее неполноту. Свойство О.-н. сильнее свойства простой непротиворечивости. Простая непротиворечивость получится, если взять в качестве (х).формулу, не содержащую х. Из теоремы Гёделя о неполноте вытекает существование непротиворечивых, но омега-противоречивых систем.

Лит.:[1] К л и н и С. К., Введение в метаматематику, пер. с англ., М., 1957. . В. Н. Гришин.