ОБРАТНАЯ ФУНКЦИЯ

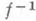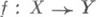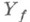- функция, определенная на множестве значений заданной функции и ставящая в соответствие каждому его элементу множество всех тех элементов из области определения рассматриваемой функции, к-рые в него отображаются, т. е. его полный прообраз. Если данная функция обозначена символом f, то О. ф. обозначается символом . Таким образом, если и - множество значений функции f, ,то для любого справедливо равенство

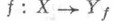Если для любого элемента его полный прообраз состоит в точности из одного элемента , т. е. отображение является биекцией, то О. ф. является однозначной, в противном случае - многозначной.

Если множества Xи Yявляются подмножествами числовой прямой (или вообще нек-рых упорядоченных множеств), то условие строгой монотонности функции f необходимо и достаточно для существования обратной однозначной функции.

По ряду свойств функции f можно судить о соответствующих свойствах О. ф. Так, напр., если функция f строго монотонна и непрерывна на нек-ром промежутке числовой оси, то ее О. ф. также монотонна и непрерывна на соответствующем промежутке. Если взаимно однозначное отображение бикомпакта на топологическое хаусдорфово пространство непрерывно, то и обратное отображение непрерывно, т. е. рассматриваемое отображение является гомеоморфизмом. Когда отображение f является биективным линейным ограниченным оператором, отображающим банахово пространство Xна банахово пространство Y, то обратный оператор также является линейным и ограниченным.

Пусть f - непрерывное отображение замыкания i 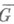ограниченной области с достаточно хорошей границей в , f - дифференцируемо в Gи отображает границу Gна границу f(G) и множество нулей его якобиана образует изолированное множество; тогда если отображение f взаимно однозначно на границе области G, то оно взаимно однозначно и на Для существования локального обратного отображения в окрестности данной точки достаточно необращения в нуль якобиана отображения в нек-рой окрестности этой точки. 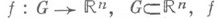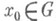Если - дифференцируемое отображение с якобианом, неравным нулю во всех точках , то для любой точки существует такая ее окрестность 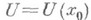, что сужение 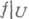отображения f на окрестности Uвзаимно однозначно отображает множество Uна нек-рую окрестность точки и обратное отображениетакже 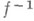дифференцируемо (на V). Эта теорема обобщается и на бесконечномерный случай: пусть Xи Y - полные нормированные пространства,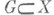- открытое множество, 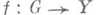- непрерывно дифференцируемое отображение. Если - обратимый элемент пространства линейных ограниченных операторов производная Фреше),то существуют-такие окрестности соответственно точек х ₀ и в пространствах Xп. Y, что отображение 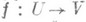является непрерывно дифференцируемым гомеоморфизмом вместе со своим обратным отображением. Лит.:[1] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 5 изд., М.. 1981; [2] Шварц Л., Анализ, пер. С франц., т. 1, М., 1972.

Л. Д. Кудрявцев.