ОБЛАСТЬ

ОБЛАСТЬ

-непустое связное открытое множество точек топологич. пространства . Замыкание области Dная. замкнутой областью; замкнутое множество наз. границей О. D. Точки наз. также внутренними точками О. D; точки наз. граничными точками для О. D;. точки дополнения - внешними точками для О. D.

Любые две точки О. Dдействительного евклидова пространства (либо комплексного пространства либо римановой поверхности или римановой области), можно соединить путем (или дугой), целиком расположенным в D, а в случае или - даже ломаной линией с конечным числом звеньев. Конечные и бесконечные открытые интервалы - единственные О. на числовой прямой 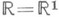; их границы состоят не более чем из двух точек. Область Dна плоскости наз. односвязной, если любой замкнутый путь в Dможно непрерывно деформировать в точку, оставаясь все время вО . D. Вообще говоря, граница односвязной О. открытой плоскост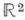и или

может состоять из любого числа ксвязных компонент, 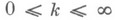. Если же Dрассматривается как О. компактной расширенной плоскост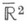и или и число ккомпонент границы конечно, то кназ. порядком связности плоской О. D;при 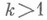О. Dназ. мвогосвязной. Иначе говоря, порядок связности кна единицу больше минимального числа разрезов, попарно соединяющих компоненты границы, к-рые нужно провести, чтобы превратить О. D в односвязную. При k=2 О. наз. двусвязной, при k=3 - трехсвязной и т. <д.; при имеем конечносвязные О., при 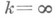- бесконечносвязные О. Порядок связности плоской О. характеризует ее топологический тип. Топологич. типы О. пространств нельзя характеризовать каким-либо одним числом.

Даже в случае односвязной плоской О. метрич. строение ее границы 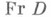может быть очень сложным (см. Граничные элементы). В частности, точки границы делятся на достижимые точки для к-рых существует путь , соединяющий 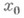в Dс любой точкой , и недостижимые точки, для к-рых такого пути не существует. Множество достижимых точек границы Fr Dлюбой плоской односвязной О. всюду плотно на Fr D.

Область Dпространства 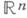или наз. ограниченной, или конечной, если

в противном случае О. Dназ неограниченной, или бесконечной. Замкнутая жорданова плоская кривая разделяет плоскость 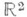или на две жордановы О.: конечную и бесконечную 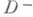. Все граничные точки жордановых О. достижимы.

Е. Д. Соломенцев.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужно сделать НИР?
Синонимы:
, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,


Полезное


Смотреть что такое "ОБЛАСТЬ" в других словарях:

  • область — область, и, мн. ч. и, ей …   Русский орфографический словарь

  • ОБЛАСТЬ — ОБЛАСТЬ, области, мн. областей, жен. 1. Часть страны, территория, пространство. Область за областью покрываются сетью дорог. На севере целые области покрыты лесами. «Подговаривал казаков бежать в области турецкого султана.» Пушкин. 2. Крупная… …   Толковый словарь Ушакова

  • ОБЛАСТЬ — жен. (об власть) великая власть, широкая сила, право и мочь. Коею областию сие твориши, кем дана тебе власть, откуда она? Область бесов изгонять. | Страна, земля, государство; | у нас, край под особым управлением, не названный губернией; вновь… …   Толковый словарь Даля

  • область — Край, округ, сторона, страна, земля, территория; круг, сфера ведомство, среда, царство. Ср. круг, страна... Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999 …   Словарь синонимов

  • Область — один из шести видов субъектов РФ. Область образуются на территориальной основе. Область имеет свой устав и законодательство. См. также: Субъекты Российской Федерации Финансовый словарь Финам …   Финансовый словарь

  • Область H I — Область H I  межзвёздное облако, состоящее из атомарного водорода (H I). Эти области являются неизлучающими, за исключением эмиссии на длине волны 21 см (1 420 МГц) (Линия водорода). У этой линии очень низкая вероятность перехода, поэтому… …   Википедия

  • ОБЛАСТЬ — внутримышечных инъекций. Жарг. мол. Шутл. Ягодицы. Максимов, 280. Отходить в область преданий. Книжн. Становиться далёким прошлым. Ф 2, 30 …   Большой словарь русских поговорок

  • ОБЛАСТЬ — 1) в Российской империи административная единица, расположенная на приграничной территории и на землях казачьих войск, соответствует губернии. Обычно входила в генерал губернаторства; 2) в СССР основная административно территориальная единица со… …   Юридический словарь

  • ОБЛАСТЬ — 1) в Российской империи административная единица (20 областей), соответствовавшая губернии, расположенная на приграничных территориях и на землях казачьих войск. Обычно входила в генерал губернаторства.2) В СССР, Российской Федерации основная… …   Большой Энциклопедический словарь

  • ОБЛАСТЬ — ОБЛАСТЬ, в математике набор значений, которые можно приписать независимой переменной в функции или зависимости, причем набор, или множество, значений зависимой переменной называется диапазоном. Например, если взять функцию у=х2, где х принимает… …   Научно-технический энциклопедический словарь

  • ОБЛАСТЬ — ОБЛАСТЬ, и, мн. и, ей, жен. 1. Часть страны, государственной территории (или территорий). Южные области России. Северные области Европы. 2. Крупная административно территориальная единица. Автономная о. Московская о. Начальство из области (из… …   Толковый словарь Ожегова


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»