- НЕРАВЕНСТВО
- отношение, связывающее два числа
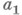 и
и  посредством одного из знаков:
посредством одного из знаков:  (меньше),
(меньше), (меньше или равно),
(меньше или равно),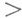 (больше),
(больше), (больше или равно),
(больше или равно), 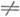 (неравно), то есть
(неравно), то есть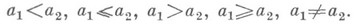
Иногда несколько Н. записываются вместе, напр.

Н. обладают многими свойствами, общими с равенствами. Так, Н. остается справедливым, если к обеим частям его прибавить (или от обеих частей отнять) одно и то же число. Точно так же можно умножить обе части Н. на одно и то же положительное число. Однако если обе части Н. умножить на отрицательное число, то смысл Н. изменится на противоположный (т. е. знак
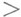 заменяется на
заменяется на  , а
, а  на
на  ). Из неравенств
). Из неравенств 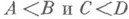 следует
следует 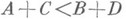 и
и  , т. е. одноименные Н. (
, т. е. одноименные Н. (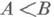 и
и  ) можно почленно складывать, а разноименные Н. (
) можно почленно складывать, а разноименные Н. (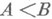 и
и 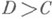 ) - почленно вычитать. Если числа
) - почленно вычитать. Если числа 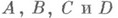 положительны, то из неравенств
положительны, то из неравенств  и
и  следует также
следует также  и
и 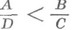 , т. е. одноименные Н. (между положительными числами) можно почленно перемножать, а разноименные - почленно делить.
, т. е. одноименные Н. (между положительными числами) можно почленно перемножать, а разноименные - почленно делить.Н., в к-рые входят величины, принимающие различные числовые значения, могут быть верны для одних значений этих величин и неверны для других. Так, неравенство
 верно при
верно при  и неверно при x=2. Для Н. этого типа возникает вопрос об их решении, т. е. об определении границ, в к-рых следует брать входящие в Н. величины для того, чтобы Н. были справедливы. Так, переписывая неравенство
и неверно при x=2. Для Н. этого типа возникает вопрос об их решении, т. е. об определении границ, в к-рых следует брать входящие в Н. величины для того, чтобы Н. были справедливы. Так, переписывая неравенство  в виде:
в виде:  замечают, что оно будет верно для всех х, удовлетворяющих одному из следующих неравенств:
замечают, что оно будет верно для всех х, удовлетворяющих одному из следующих неравенств: 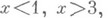 к-рые и являются решением данного Н.
к-рые и являются решением данного Н.Ниже приводятся нек-рые Н., выполняющиеся тождественно в той или иной области изменения входящих в них переменных.
1) Неравенство для модулей. Для любых действительных или комплексных чисел

 справедливо Н.
справедливо Н.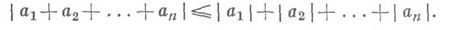
. 2) Неравенство для средних. Наиболее известны Н., связывающие гармоническое, геометрическое, арифметическое и квадратичное средние:

здесь все числа
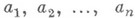 - положительны.
- положительны.3) Неравенства для сумм и их интегральные аналоги. Таковы, напр., Вуняковского неравенство, Гёльдера неравенство, Гильберта неравенство, Коши неравенство.
4) Неравенства для степеней чисел. Наиболее известно здесь Минковского неравенство и его обобщения на случай рядов и интегралов.
5) Неравенства для некоторых классов последовательностей и функций. Примерами могут служить Чебышева неравенство для монотонных последовательностей и Иенсена неравенство для выпуклых функций.
6) Неравенство для определителей. Напр., неравенство Ада мара - см. Адамара теорема об определителях.
7) Линейные неравенства. Рассматривается система Н. вида
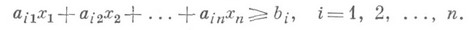
Совокупность решений этой системы Н. представляет собой нек-рый выпуклый многогранник в n-мерном пространстве (
 ); задача теории линейных неравенств состоит в том, чтобы изучить свойства этого многогранника.
); задача теории линейных неравенств состоит в том, чтобы изучить свойства этого многогранника.Н. имеют существенное значение для всех разделов математики. В теории чисел целый раздел этой дисциплины - диофантовы приближения- полностью основан на Н.; аналитич. теория чисел тоже часто оперирует с Н. (см., напр., Виноградова оценки). В геометрии Н. постоянно встречаются в теории выпуклых тел и в изопериметрич. задаче (см. Изопериметрическое неравенство, Изопериметрическое неравенство классическое). В теории вероятностей многие законы формулируются с помощью Н. (см., напр., Чебышева неравенство и его обобщение Колмогорова неравенство). В теории дифференциальных уравнений используются т. н. дифференциальные неравенства. В теории функций постоянно употребляются различные Н. для производных от многочленов и тригонометрич. полиномов (см., напр., Вернштейна неравенство, Джексона неравенство);о Н., связанных с вложением классов дифференцируемых функций, см. Колмогорова неравенство, Вложения теоремы. В функциональном анализе при определении нормы в функциональном пространстве требуется, чтобы она удовлетворяла Н. треугольника
 . Многие классич. Н. в сущности определяют значения нормы линейного функционала или линейного оператора в том или ином пространстве или дают оценки для них (см., напр., Бесселя неравенство, Минковского неравенство). В вычислительной математике Н. применяются для оценки погрешности приближенного решения задачи.
. Многие классич. Н. в сущности определяют значения нормы линейного функционала или линейного оператора в том или ином пространстве или дают оценки для них (см., напр., Бесселя неравенство, Минковского неравенство). В вычислительной математике Н. применяются для оценки погрешности приближенного решения задачи.Лит.:Харди Г. Г., Литтльвуд Д ж. Е., Полиа Г., Неравенства, пер. с англ., М., 1948; Беккен6ах Э., Беллмав Р., Неравенства, пер. с англ., М., 1965.
По материалам одноименной статьи из БСЭ-3.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
