МОНОТОННАЯ БУЛЕВА

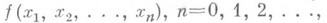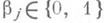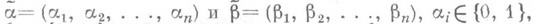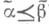ФУНКЦИЯ - булева функция обладающая следующим свойством: если для нек-рых наборов ,выполнено условие для всех i(в этом случае пишут ), то 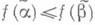. Напр., функция (сложение по модулю 2) не является монотонной, т. к. 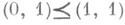, но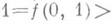

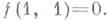
Примеры М. б. ф.: константы 0 и 1, тождественная функция 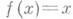, дизъюнкция конъюнкция 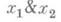и т. д. Примеры немонотонных булевых функций: отрицание 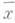, импликация и т. д. Любая функция, полученная с помощью операции суперпозиции из М. б. <ф., сама является монотонной. Другими словами, класс всех М. б. ф. является замкнутым. Более того, класс всех М. б. ф. является одним из пяти максимальных (предполных) классов в множестве всех булевых функций, т. е. не существует замкнутого класса булевых функций, содержащего все М. б. ф. и отличного от класса М. б. ф. и класса всех булевых функций. Сокращенная дизъюнктивная нормальная форма любой М. б. ф., отличной от констант 0 и 1, не содержит отрицаний переменных. Множество функций является полной системой (и, более того, базисом) в классе всех М. б. ф.

Для числа М. б. ф., зависящих от ппеременных, известно, что где , с- нек-рая константа (см. [2]).

Для сложности реализации класса М. б. ф. схемами из функциональных элементов и контактными схемами получены более низкие значения, чем для сложности реализации произвольных булевых функций (см. Синтеза задачи). Нек-рые дискретные экстремальные задачи сводятся к задаче расшифровки М. б. ф. В этой задаче требуется, зная, что нек-рая функция является М. б. ф., выяснить ее значения на всех наборах, задав как можно меньше вопросов вида: "Чему равно значение 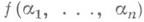на нек-ром наборе ". Был предложен [3] алгоритм, к-рый требует для расшифровки произвольной М. б. ф. задания не более вопросов. С другой стороны, не существует алгоритма расшифровки, к-рый отличал бы функцию

от всех остальных М. б. ф. менее чем за вопросов.

Обобщением понятия М. б. ф. являются монотонные функции k- значной логики. Если на множестве задано произвольное частичное упорядочение 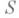(пишут ), то, по определению, для любых двух наборов и запись означает, что для всех i. Функция k-значной логики (т. е. определенная и принимающая значение на Е _k )наз. монотонной относительно S, если для любых наборов и из условия вытекает . Класс всех функций, монотонных относительно нек-рого частичного упорядочения на , всегда является замкнутым классом; он является предполным классом в k-значной логике в том и только в том случае, если в Sимеются ровно один минимальный и ровно один максимальный элементы. Для числа функций k-значной логики, зависящих от ппеременных и монотонных относительно S, при имеет место соотношение

где С(S)- константа, эффективно вычисляемая по данному частичному упорядочению S(см. [5]).

Лит.:[1] Яблонский С. В., Введение в дискретную математику, М., 1979; [2] Клейтмен Д., "Кибернетич. сб.", 1970, в. 7, с. 43-52;[3]Ансел Ж., там же, 1968, в. 5,с.47 -52, 53-57, 58-63; [4] Мартынюк В. В., "Проблемы кибернетики", 1960, в. 3, с. 49-60; [5] Алексеев В. Б., там же, 1974, в. 28, с. 5-24.

В. Б. Алексеев.