- МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
- раздел математич. статистики, посвященный математич. методам построения оптимальных планов сбора, систематизации и обработки многомерных статистич. данных, направленным на выявление характера и структуры взаимосвязей между компонентами исследуемого многомерного признака и предназначенным для получения научных и практич. выводов. Под многомерным признаком понимается р-мерный вектор

 показателей (признаков, переменных)
показателей (признаков, переменных) среди к-рых могут быть: количественные, т. е. скалярно измеряющие в определенной шкале степень проявления изучаемого свойства объекта, п о-рядковые (или ординальные), т. е. позволяющие упорядочивать анализируемые объекты по степени проявления в них изучаемого свойства; и классификационные (или номинальные), т. е. позволяющие разбивать исследуемую совокупность объектов на не поддающиеся упорядочиванию однородные (по анализируемому свойству) классы. Результаты измерения этих показателей
среди к-рых могут быть: количественные, т. е. скалярно измеряющие в определенной шкале степень проявления изучаемого свойства объекта, п о-рядковые (или ординальные), т. е. позволяющие упорядочивать анализируемые объекты по степени проявления в них изучаемого свойства; и классификационные (или номинальные), т. е. позволяющие разбивать исследуемую совокупность объектов на не поддающиеся упорядочиванию однородные (по анализируемому свойству) классы. Результаты измерения этих показателей
на каждом из побъектов исследуемой совокупности образуют последовательность многомерных наблюдений, или исходный массив многомерных данных для проведения М. с. а. Значительная часть М. с. а. обслуживает ситуации, в к-рых исследуемый многомерный признак
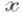 интерпретируется как многомерная случайная величина и соответственно последовательность многомерных наблюдений (1) - как выборка из генеральной совокупности. В этом случае выбор методов обработки исходных статистич. данных и анализ их свойств производится на основе тех или иных допущений относительно природы многомерного (совместного) закона распределения вероятностей
интерпретируется как многомерная случайная величина и соответственно последовательность многомерных наблюдений (1) - как выборка из генеральной совокупности. В этом случае выбор методов обработки исходных статистич. данных и анализ их свойств производится на основе тех или иных допущений относительно природы многомерного (совместного) закона распределения вероятностей 
По содержанию М. с. а. может быть условно разбит на три основных подраздела: М. с. а. многомерных распределений и их основных характеристик; М. с. а. характера и структуры взаимосвязей между компонентами исследуемого многомерного признака; М. с. а. геометрич. структуры исследуемой совокупности многомерных наблюдений.
Многомерный статистический анализ многомерных распределений и их основных характеристик охватывает лишь ситуации, в к-рых обрабатываемые наблюдения (1) имеют вероятностную природу, т. е. интерпретируются как выборка из соответствующей генеральной совокупности. К основным задачам этого подраздела относятся: статистич. оценивание исследуемых многомерных распределений, их основных числовых характеристик и параметров; исследование свойств используемых статистич. оценок; исследование распределений вероятностей для ряда статистик, с помощью к-рых строятся статистич. критерии проверки различных гипотез о вероятностной природе анализируемых многомерных данных. Основные результаты относятся к частному случаю, когда исследуемый признак
 подчинен многомерному нормальному закону распределения
подчинен многомерному нормальному закону распределения  функция плотности к-рого
функция плотности к-рого  задается соотношением
задается соотношением
где
 - вектор математич. ожиданий компонент случайной величины
- вектор математич. ожиданий компонент случайной величины  , т. е.
, т. е.
 - ковариационная матрица случайного вектора
- ковариационная матрица случайного вектора 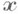 , т. е.
, т. е.
 - ковариации компонент вектора
- ковариации компонент вектора  (рассматривается невырожденный случай, когда ранг
(рассматривается невырожденный случай, когда ранг  ; в противном случае, т. е. при ранге
; в противном случае, т. е. при ранге  , все результаты остаются справедливыми, но применительно к подпространству меньшей размерности
, все результаты остаются справедливыми, но применительно к подпространству меньшей размерности  , в к-рой оказывается сосредоточенным распределение вероятностей исследуемого случайного вектора
, в к-рой оказывается сосредоточенным распределение вероятностей исследуемого случайного вектора  ).
).Так, если (1) - последовательность независимых наблюдений, образующих случайную выборку из
 то оценками максимального правдоподобия для параметров
то оценками максимального правдоподобия для параметров 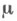 и
и  , участвующих в (2), являются соответственно статистики (см. [1], [2])
, участвующих в (2), являются соответственно статистики (см. [1], [2])
и

причем случайный вектор
 подчиняется р-мерному нормальному закону
подчиняется р-мерному нормальному закону  и не зависит от
и не зависит от  , а совместное распределение элементов матрицы
, а совместное распределение элементов матрицы  описывается т. н. распределением Уиша р-т а (см. [4]), плотность к-рого
описывается т. н. распределением Уиша р-т а (см. [4]), плотность к-рого
В рамках этой же схемы исследованы распределения и моменты таких выборочных характеристик многомерной случайной величины, как коэффициенты парной, частной и множественной корреляции, обобщенная дисперсия (т. е. статистика
 ), обобщенная
), обобщенная  -статистике Хотеллинга (см. [5]). В частности (см. [1]), если определить в качестве выборочной ковариационной матрицы
-статистике Хотеллинга (см. [5]). В частности (см. [1]), если определить в качестве выборочной ковариационной матрицы  подправленную "на несмещенность" оценку
подправленную "на несмещенность" оценку  , а именно:
, а именно:
то распределение случайной величины
 стремится к
стремится к  при
при  , а случайные величины
, а случайные величины
и

подчиняются F-распределениям с числами степеней свободы соответственно (р, п-р) и (р, п 1+п 2 -р-1). В соотношении (7) п 1 и n2 - объемы двух независимых выборок вида (1), извлеченных из одной и той же генеральной совокупности
 - оценки вида (3) и (4)-(5), построенные по i-й выборке, а
- оценки вида (3) и (4)-(5), построенные по i-й выборке, а 
- общая выборочная ковариационная матрица, построенная по оценкам
 и
и 
Многомерный статистический анализ характера и структуры взаимосвязей компонент исследуемого многомерного признака объединяет в себе понятия и результаты, обслуживающие такие методы и модели М. с. а., как множественная регрессия, многомерный дисперсионный анализ и ковариационный анализ, факторный анализ и метод главных компонент, анализ канонич. корреляций. Результаты, составляющие содержание этого подраздела, могут быть условно разделены на два основных типа.
1) Построение наилучших (в определенном смысле) статистич. оценок для параметров упомянутых моделей и анализ их свойств (точности, а в вероятностной постановке - законов их распределения, доверительных: областей и т. д.). Так, пусть исследуемый многомерный признак
 интерпретируется как векторная случайная величина, подчиненная р-мерному нормальному распределению
интерпретируется как векторная случайная величина, подчиненная р-мерному нормальному распределению  , и расчленен на два подвектора--столбца
, и расчленен на два подвектора--столбца  и
и  размерности qи р-qсоответственно. Это определяет и соответствующее расчленение вектора математич. ожиданий
размерности qи р-qсоответственно. Это определяет и соответствующее расчленение вектора математич. ожиданий  , теоретической и выборочной ковариационных матриц
, теоретической и выборочной ковариационных матриц  , а именно:
, а именно: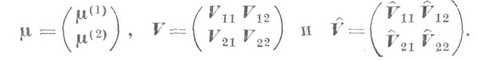
Тогда (см. [1], [2]) условное распределение подвектора
 (при условии, что второй подвектор принял фиксированное значение
(при условии, что второй подвектор принял фиксированное значение  ) будет также нормальным
) будет также нормальным  ). При этом оценками максимального правдоподобия .
). При этом оценками максимального правдоподобия . для матриц регрессионных коэффициентов
для матриц регрессионных коэффициентов  и ковариацин
и ковариацин  этой классической многомерной модели множественной регрессии
этой классической многомерной модели множественной регрессии
будут взаимно независимые статистики соответственно

здесь распределение оценки
 подчинено нормальному закону
подчинено нормальному закону  , а оценки п
, а оценки п  - закону Уишарта с параметрами
- закону Уишарта с параметрами  и
и  (элементы ковариационной матрицы
(элементы ковариационной матрицы  выражаются в терминах элементов матрицы
выражаются в терминах элементов матрицы  ).
).Основные результаты по построению оценок параметров и исследованию их свойств в моделях факторного' анализа, главных компонент и канонич. корреляций относятся к анализу вероятностно-статистич. свойств собственных (характеристических) значений и векторов различных выборочных ковариационных матриц.
В схемах, не укладывающихся в рамки классич. нормальной модели и тем более в рамки какой-либо вероятностной модели, основные результаты относятся к построению алгоритмов (и исследованию их свойств) вычисления оценок параметров, наилучших с точки зрения нек-poro экзогенно заданного функционала качества (пли адекватности) модели.
2) Построение статистич. критериев для проверки различных гипотез о структуре исследуемых взаимосвязей. В рамках многомерной нормальной модели (последовательности наблюдений вида (1) интерпретируются как случайные выборки из соответствующих многомерных нормальных генеральных совокупностей) построены, напр., статистич. критерии для проверки следующих гипотез.
I. Гипотезы
 о равенстве вектора математич. ожиданий исследуемых показателей заданному конкретному вектору
о равенстве вектора математич. ожиданий исследуемых показателей заданному конкретному вектору  ; проверяется с помощью
; проверяется с помощью  -статистики Хотеллинга с подстановкой в формулу (6)
-статистики Хотеллинга с подстановкой в формулу (6)
II. Гипотезы
 о равенстве векторов математич. ожиданий в двух генеральных совокупностях (с одинаковыми, но неизвестными ковариационными матрицами), представленных двумя выборками; проверяется с помощью статистики
о равенстве векторов математич. ожиданий в двух генеральных совокупностях (с одинаковыми, но неизвестными ковариационными матрицами), представленных двумя выборками; проверяется с помощью статистики  (см. [7]).
(см. [7]).III. Гипотезы
 о равенстве векторов математич. ожиданий в нескольких генеральных совокупностях (с одинаковыми, но неизвестными ковариационными матрицами), представленных своими выборками; проверяется с помощью статистики
о равенстве векторов математич. ожиданий в нескольких генеральных совокупностях (с одинаковыми, но неизвестными ковариационными матрицами), представленных своими выборками; проверяется с помощью статистики
в к-рой
 есть i-е р-мерное наблюдение в выборке объема
есть i-е р-мерное наблюдение в выборке объема  , представляющей j-ю генеральную совокупность, а
, представляющей j-ю генеральную совокупность, а  и
и  - оценки вида (3), построенные соответственно отдельно по каждой из выборок и по объединенной выборке объема
- оценки вида (3), построенные соответственно отдельно по каждой из выборок и по объединенной выборке объема 
IV. Гипотезы

 об эквивалентности нескольких нормальных генеральных совокупностей, представленных своими выборками
об эквивалентности нескольких нормальных генеральных совокупностей, представленных своими выборками  проверяется с помощью статистики
проверяется с помощью статистики
в к-рой
 - оценка вида (4), построенная отдельно по наблюдениям j- йвыборки, j=1, 2, ... , k.
- оценка вида (4), построенная отдельно по наблюдениям j- йвыборки, j=1, 2, ... , k.V. Гипотезы о взаимной независимости подвекторов-столбцов
 размерностей соответственно
размерностей соответственно  на к-рые расчленен исходный р-мерный вектор исследуемых показателей
на к-рые расчленен исходный р-мерный вектор исследуемых показателей 
 проверяется с помощью статистики
проверяется с помощью статистики
в к-рой
 и
и  - выборочные ковариационные матрицы вида (4) для всего вектора
- выборочные ковариационные матрицы вида (4) для всего вектора  и для его подвектора x(i) соответственно.
и для его подвектора x(i) соответственно.Многомерный статистический анализ геометрической структуры исследуемой совокупности многомерных наблюдений объединяет в себе понятия и результаты таких моделей и схем, как дискриминантный анализ, смеси вероятностных распределений, кластер-анализ и таксономия, многомерное шкалирование. Узловым во всех этих схемах является понятие расстояния (меры близости, меры сходства) между анализируемыми элементами. При этом анализируемыми могут быть как реальные объекты, на каждом из к-рых фиксируются значения показателей
 ,- тогда геометрич. образом i-го обследованного объекта будет точка
,- тогда геометрич. образом i-го обследованного объекта будет точка 
 в соответствующем р-мерном пространстве, так и сами показатели
в соответствующем р-мерном пространстве, так и сами показатели  - тогда геометрич. образом l-го показателя будет точка
- тогда геометрич. образом l-го показателя будет точка 
 в соответствующем n-мерном пространстве.
в соответствующем n-мерном пространстве.Методы и результаты дискриминантного анализа (см. [1], [2], [7]) направлены на решение следующей задачи. Известно о существовании определенного числа
 генеральных совокупностей и у исследователя имеется по одной выборке из каждой совокупности ("обучающие выборки"). Требуется построить основанное на имеющихся обучающих выборках наилучшее в определенном смысле классифицирующее правило, позволяющее приписать нек-рый новый элемент (наблюдение
генеральных совокупностей и у исследователя имеется по одной выборке из каждой совокупности ("обучающие выборки"). Требуется построить основанное на имеющихся обучающих выборках наилучшее в определенном смысле классифицирующее правило, позволяющее приписать нек-рый новый элемент (наблюдение  ) к своей генеральной совокупности в ситуации, когда исследователю заранее не известно, к какой из совокупностей этот элемент принадлежит. Обычно под классифицирующим правилом понимается последовательность действий: по вычислению скалярной функции от исследуемых показателей, по значениям к-рой принимается решение об отнесении элемента к одному из классов (построение дискриминантной функции); по упорядочению самих показателей по степени их информативности с точки зрения правильного отнесения элементов к классам; по вычислению соответствующих вероятностей ошибочной классификации.
) к своей генеральной совокупности в ситуации, когда исследователю заранее не известно, к какой из совокупностей этот элемент принадлежит. Обычно под классифицирующим правилом понимается последовательность действий: по вычислению скалярной функции от исследуемых показателей, по значениям к-рой принимается решение об отнесении элемента к одному из классов (построение дискриминантной функции); по упорядочению самих показателей по степени их информативности с точки зрения правильного отнесения элементов к классам; по вычислению соответствующих вероятностей ошибочной классификации.Задача анализа смесей распределений вероятностей (см. [7]) чаще всего (но не всегда) возникает также в связи с исследованием "геометрической структуры" рассматриваемой совокупности. При этом понятие r-го однородного класса формализуется с помощью генеральной совокупности, описываемой нек-рым (как правило, унимодальным) законом распределения
 так что распределение общей генеральной совокупности, из к-рой извлечена выборка (1), описывается смесью распределений вида
так что распределение общей генеральной совокупности, из к-рой извлечена выборка (1), описывается смесью распределений вида  где pr - априорная вероятность (удельный вес элементов) r-го класса в общей генеральной совокупности. Задача состоит в "хорошем" статистич. оценивании (по выборке
где pr - априорная вероятность (удельный вес элементов) r-го класса в общей генеральной совокупности. Задача состоит в "хорошем" статистич. оценивании (по выборке 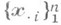 ) неизвестных параметров
) неизвестных параметров  а иногда и к. Это, в частности, позволяет свести задачу классификации элементов к схеме дискриминантного анализа, хотя в данном случае отсутствовали обучающие выборки.
а иногда и к. Это, в частности, позволяет свести задачу классификации элементов к схеме дискриминантного анализа, хотя в данном случае отсутствовали обучающие выборки.Методы и результаты кластер-анализа (классификации, таксономии, распознавании образов "без учителя", см. [2], [6], [7]) направлены на решение следующей задачи. Геометрич. структура анализируемой совокупности элементов задана либо координатами соответствующих точек (т. е. матрицей
 ... , п), либо набором геометрич. характеристик их взаимного расположения, напр, матрицей попарных расстояний
... , п), либо набором геометрич. характеристик их взаимного расположения, напр, матрицей попарных расстояний  . Требуется разбить исследуемую совокупность элементов на сравнительно небольшое (заранее известное или нет) число классов так, чтобы элементы одного класса находились на небольшом расстоянии друг от друга, в то время как разные классы были бы по возможности достаточно взаимоудалены один от другого и не разбивались бы на столь же удаленные друг от друга части.
. Требуется разбить исследуемую совокупность элементов на сравнительно небольшое (заранее известное или нет) число классов так, чтобы элементы одного класса находились на небольшом расстоянии друг от друга, в то время как разные классы были бы по возможности достаточно взаимоудалены один от другого и не разбивались бы на столь же удаленные друг от друга части.Задача многомерного шкалирования (см. [6]) относится к ситуации, когда исследуемая совокупность элементов задана с помощью матрицы попарных расстояний
 и заключается в приписывании каждому из элементов заданного числа (р)координат таким образом, чтобы структура попарных взаимных расстояний между элементами, измеренных с помощью этих вспомогательных координат, в среднем наименее отличались бы от заданной. Следует заметить, что основные результаты и методы кластер-анализа и многомерного шкалирования развиваются обычно без каких-либо допущении о вероятностной природе исходных данных.
и заключается в приписывании каждому из элементов заданного числа (р)координат таким образом, чтобы структура попарных взаимных расстояний между элементами, измеренных с помощью этих вспомогательных координат, в среднем наименее отличались бы от заданной. Следует заметить, что основные результаты и методы кластер-анализа и многомерного шкалирования развиваются обычно без каких-либо допущении о вероятностной природе исходных данных.Прикладное назначение многомерного статистического анализа состоит в основном в обслуживании следующих трех проблем.
Проблема статистического исследования зависимостей между анализируемыми показателями. Предполагая, что исследуемый набор статистически регистрируемых показателей xразбит, исходя из содержательного смысла этих показателей и окончательных целей исследования, на q-мернын подвектор
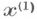 предсказываемых (зависимых) переменных и (р-q)-мерный подвектор
предсказываемых (зависимых) переменных и (р-q)-мерный подвектор  предсказывающих (независимых) переменных, можно сказать, что проблема состоит в определении на основании выборки (1) такой q-мерной векторной функции
предсказывающих (независимых) переменных, можно сказать, что проблема состоит в определении на основании выборки (1) такой q-мерной векторной функции  из класса допустимых решений F, к-рая давала бы наилучшую, в определенном смысле, аппроксимацию поведения подвектора показателей
из класса допустимых решений F, к-рая давала бы наилучшую, в определенном смысле, аппроксимацию поведения подвектора показателей  . В зависимости от конкретного вида функционала качества аппроксимации и природы ,анализируемых показателей приходят к тем или иным схемам множественной регрессии, дисперсионного, ковариационного или конфлюентного анализа.
. В зависимости от конкретного вида функционала качества аппроксимации и природы ,анализируемых показателей приходят к тем или иным схемам множественной регрессии, дисперсионного, ковариационного или конфлюентного анализа.Проблема классификации элементов (объектов или показателей) в общей (нестрогой) постановке заключается в том, чтобы всю анализируемую совокупность элементов, статистически представленную в виде матрицы
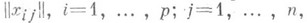 или матрицы
или матрицы  разбить на сравнительно небольшое число однородных, в определенном смысле, групп [7]. В зависимости от природы априорной информации и конкретного вида функционала, задающего критерий качества классификации, приходят к тем или иным схемам дискриминантного анализа, кластер-анализа (таксономии, распознавания образов "без учителя"), расщепления смесей распределений.
разбить на сравнительно небольшое число однородных, в определенном смысле, групп [7]. В зависимости от природы априорной информации и конкретного вида функционала, задающего критерий качества классификации, приходят к тем или иным схемам дискриминантного анализа, кластер-анализа (таксономии, распознавания образов "без учителя"), расщепления смесей распределений.Проблема снижения размерности исследуемого факторного пространства и отбора наиболее информативных показателей заключается в определении такого набора сравнительно небольшого числа
 показателен
показателен  найденного в классе допустимых преобразований
найденного в классе допустимых преобразований  исходных показателей
исходных показателей 
 на к-ром достигается верхняя грань нек-рой экзогенно заданной меры информативности m-мерной системы признаков (см. [7]). Конкретизация функционала, задающего меру автоинформативности (т. е. нацеленное на максимальное сохранение информации, содержащейся в статистич. массиве (1) относительно самих исходных признаков), приводит, в частности, к различным схемам факторного анализа и главных компонент, к методам экстремальной группировки признаков. Функционалы, задающие меру внешней информативности, т. е. нацеленные на извлечение из (1) максимальной информации относительно нек-рых других, не содержащихся непосредственно в ж, показателен или явлений, приводят к различным методам отбора наиболее информативных показателей в схемах статистич. исследования зависимостей и дискриминантного анализа.
на к-ром достигается верхняя грань нек-рой экзогенно заданной меры информативности m-мерной системы признаков (см. [7]). Конкретизация функционала, задающего меру автоинформативности (т. е. нацеленное на максимальное сохранение информации, содержащейся в статистич. массиве (1) относительно самих исходных признаков), приводит, в частности, к различным схемам факторного анализа и главных компонент, к методам экстремальной группировки признаков. Функционалы, задающие меру внешней информативности, т. е. нацеленные на извлечение из (1) максимальной информации относительно нек-рых других, не содержащихся непосредственно в ж, показателен или явлений, приводят к различным методам отбора наиболее информативных показателей в схемах статистич. исследования зависимостей и дискриминантного анализа.Основной математический инструментарий М. с. а. составляют специальные методы теории систем линейных уравнений и теории матриц (методы решения простой и обобщенной задачи о собственных значениях и векторах; простое обращение и псевдообращение матриц; процедуры диагонализации матриц и т. д.) и нек-рые оптимизационные алгоритмы (методы покоординатного спуска, сопряженных градиентов, ветвей и границ, различные версии случайного поиска и стохастич. аппроксимации и т. д.).
Лит.:[1] Андерсон Т., Введение в многомерный статистический анализ, пер. с англ., М., 1963; [2] Кендалл М. Дж.., Стьюарт А., Многомерный статистический анализ и временные ряды, пер. с англ., М., 1976; [3] Большев Л. Н., "Bull. Int. Stat. Inst.", 1969, № 43, p. 425-41; [4] Wishаrt .J., "Biometrika", 1928, v. 20A, p. 32-52: [5] Hotelling H., "Ann. Math. Stat.", 1931, v. 2, p. 360-78; [в] Кruskal J. В., "Psychometrika", 1964, v. 29, p. 1-27; [7] Айвазян С. А., Бежаева 3. И., . Староверов О. В., Классификация многомерных наблюдений, М., 1974.
С. А. Айвазян.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
