МНОГОЛИСТНАЯ ФУНКЦИЯ — понятие, естественным образом обобщающее понятие однолистной функции. Функция , регулярная или мероморфная в области Dкомплексной плоскости z, наз. р листной в D(р=1, 2, ...), если она принимает в этой области каждое свое значение не более рраз,… … Математическая энциклопедия
Осока многолистная — Общий вид растения … Википедия
ОДНОЛИСТНАЯ ФУНКЦИЯ — функция f, регулярная или мероморфная в области Врасширенной комплексной плоскости п такая, что для всяких zl , выполняется соотношение то есть f отображает В в взаимно однозначно. При этом обратная функция также однолистна. Обобщением О. ф.… … Математическая энциклопедия
Теневыносливые садовые декоративные растения — Приложение к статье Теневыносливые растения В списке представлены декоративные растения, выращиваемые в садах и парках в открытом грунте и обладающие теневыносливостью. Следует иметь в виду, что представленные растения обладают этим свойством в… … Википедия
Региональный ландшафтный парк «Межреченский» — Содержание 1 Общая характеристика 2 Физико географическое районирование 3 Геол … Википедия
ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО ТЕОРИЯ — в широком смысле слова теория функций, областью определения к рых является нек рое множество точек z комплексной плоскости (функции одного комплексного переменного) или множество точек z=(z1,. . . ,zn) комплексного евклидова пространства п>1… … Математическая энциклопедия
ПЛОЩАДЕЙ ПРИНЦИП — площадь дополнения к образу области при ее отображении регулярной в ней функцией неотрицательна. Впервые П. п. использовал в 1914 Т. Гронуолл [1], к рый доказал этим путем т. н. внешнюю теорему площадей для функций класса 2 функций регулярных и… … Математическая энциклопедия
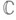, такая, что над каждой точкой ее проекции 
расположены не менее двух точек S; ветвления точка R порядка 
считается при этом за kточек. Напр., аналитич. функция 
отображает взаимно однозначно круг 
на двулистную область (двулистный круг)
римановой поверхности Вэтой функции; всюду, кроме начала координат, это отображение конформно.
