МИХАЙЛОВА КРИТЕРИЙ

все корни многочлена

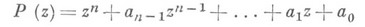
с действительными коэффициентами имеют строго отрицательные действительные части тогда и только тогда, когда комплекснозначная функция действительного переменного описывает в комплексной плоскости z кривую (годограф Михайлова), начинающуюся на положительной действительной полуоси, не попадающую в начало координат и последовательно проходящую против хода часовой стрелки пквадрантов (эквивалентное условие: когда радиус-вектор при возрастании w от 0 до нигде не обращается в нуль и монотонно поворачивается в положительном направлении на угол pn/2).

Этот критерий впервые был предложен А. В. Михайловым [1]. Он равносилен Рауса- Гурвица критерию, однако носит геометрич. характер и не требует проверки детерминантных неравенств (см. [2], [31). М. к. дает необходимое и достаточное условие асимптотич. устойчивости линейного дифференциального уравнения n-го порядка

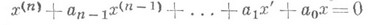
с постоянными коэффициентами или линейной системы

с постоянной матрицей А, характеристич. многочлен к-рой совпадает с Р(z) (см. [4]).

М. к.- один из частотных критериев устойчивости линейных систем автоматич. регулирования (примыкающий, напр., к Найквиста критерию). Известны обобщения М. к. на системы автоматич. регулирования с запаздыванием, на импульсные системы (см. [5]), а также аналоги М. к. для нелинейных систем управления (см. [6]).

Лит.:[1] Михайлов А. В., "Автоматика и телемеханика", 1938, № 3, с. 27-81; [2] Чеботарев Н. Г., Мейман Н. Н., Проблема Рауса - Гурвица для полиномов и целых функций, М.-Л., 1949 ("Тр. Матем. ин-та АН СССР", т. 26); [3] Лаврентьев М. А., Шабат Б. В., Методы теории Функций комплексного переменного, 4 изд., М., 1973; [4] Демидович Б. П., Лекции по математической теории устойчивости, М., 1967; [5] Гноенский Л. С, Каменский Г. А., Эльсгольц Л. Э., Математические основы теории управляемых систем, М., 1969; [6] Блакьер О., Анализ нелинейных систем, пер. с англ., М., 1969.

Н. X. Розов.