МАРКОВА ЦЕПЬ ВОЗВРАТНАЯ

МАРКОВА ЦЕПЬ ВОЗВРАТНАЯ

цепь Маркова, в к-рой случайная траектория x(t), выходящая из любого состояния x(0)=i, с вероятностью 1 возвращается когда-нибудь в это же состояние. В терминах переходных вероятностей р ij(t) возвратность цепи Маркова с дискретным временем эквивалентна расходимости при любом iряда

В М. ц. в. траектория с вероятностью 1 возвращается в состояние iбесконечное число раз. В М. ц. в. нет несущественных состояний, а все существенные состояния разбиваются на возвратные классы. Примером М. ц. в. может служить симметричное случайное блуждание по целочисленной решетке прямой или плоскости. В симметричном блуждании по прямой частица из положения хпереходит в положения 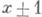свероятностями 1/2; в симметричном блуждании по плоскости частица из точки ( х, у).с вероятностями 1/4 переходит в одну из четырех соседних точек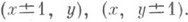

В этих примерах частица, начавшая блуждание из какой-либо точки, с вероятностью 1 возвращается в эту точку. Симметричное блуждание по целочисленной решетке трехмерного пространства, когда вероятности перехода из ( х, у,z) в соседние точки равны 1/6, невозвратно. В этом случае вероятность возвращения частицы в начальную точку равна приближенно 0,35.

Лит.:[1] Ф е л л е р В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 1, М., 1967.

Б. А. Севастьянов.



Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем сделать НИР

Полезное


Смотреть что такое "МАРКОВА ЦЕПЬ ВОЗВРАТНАЯ" в других словарях:

  • МАРКОВА ЦЕПЬ — марковский процесс с конечным или счетным множеством состояний. Теория М. ц. возникла на основе исследований А. А. Маркова, к рый в 1907 положил начало изучению последовательностей зависимых испытаний и связанных с ними сумм случайных величин [1] …   Математическая энциклопедия

  • Маркова цепь — Цепь Маркова  последовательность случайных событий с конечным или счётным бесконечным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова …   Википедия

  • Цепь Маркова — Пример цепи с двумя состояниями Цепь Маркова  последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем свойством, что, го …   Википедия

  • Цепь (матем.) — Цепь Маркова  последовательность случайных событий с конечным или счётным бесконечным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова …   Википедия

  • Возвратная цепь Маркова — Возвратное состояние это состояние Марковской цепи, посещаемое ею бесконечное число раз. Содержание 1 Определение 2 Критерий возвратности 3 Время возвращения …   Википедия

  • Цепи Маркова — Цепь Маркова  последовательность случайных событий с конечным или счётным бесконечным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова …   Википедия

  • Неразложимая цепь Маркова — Определение Пусть однородная цепь Маркова с дискретным временем. Состояние j называется достижимым из состояния i, если существует n = n(i,j) такое, что . Пишут …   Википедия

  • Периодическая цепь Маркова — Периодическое состояние это такое состояние цепи Маркова, которое навещается цепью только через промежутки времени, кратные фиксированному числу. Период состояния Пусть дана однородная цепь Маркова с дискретным временем с матрицей переходных… …   Википедия

  • Эргодическая цепь Маркова — Определение Пусть однородная цепь Маркова с дискретным временем и счётным числом состояний. Обозначим переходные вероятности за n шагов. Если существует дискретное распределение , такое что …   Википедия

  • Марковские цепи — Цепь Маркова  последовательность случайных событий с конечным или счётным бесконечным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»