ЛОРЕНЦА ПРЕОБРАЗОВАНИЕ

преобразование координат, связывающее две галилеевы системы координат в каком-либо псевдоевклидовом пространстве;иными словами, Л. п. сохраняет квадрат т. н. интервала событий. Л. п. является аналогом ортогональных преобразований (или обобщением понятия движения) в евклидовом пространстве. Л. п. образуют группу, называемую группой Лоренца (или общей группой Лоренца), к-рая обозначается через L. Л. п. находят применение в четырехмерном пространстве-времени специальной теории относительности, для к-рого в галилеевых координатах х, у, z, tинтервал имеет вид

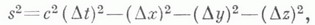
где с - скорость света в вакууме.

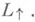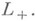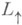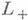Часто рассматривают более узкие классы Л. п. Так, Л. п., сохраняющие знак координаты t, образуют т. н. полную группу Лоренца Л. п., матрицы к-рых имеют положительный определитель, наз. собственными преобразованиями Лоренца и образуют собственную группу Лоренца Пересечение и часто наз. просто группой Лоренца.

Общая группа Л. п. состоит из комбинаций пространственных отражений, отражений во времени, пространственных поворотов и преобразований, к-рые с физич. точки зрения являются преобразованиями перехода от одной инерциальной системы отсчета к другой, движущейся относительно первой со скоростью V, а с ма-тематич. точки зрения - гиперболич. поворотом на угол y в плоскости с псевдоевклидовой метрикой. Наличие последнего типа преобразований является специфич. чертой группы Л. п.

Для перехода от галилеевой системы координат х', у', z', t' к галилеевой системе координат х, у, z, t, движущейся относительно первой со скоростью Vпараллельно оси х', указанные преобразования имеют вид

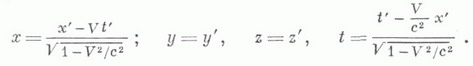
Если ввести угол гиперболического поворота y по формулам

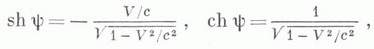
то Л. п. примут вид

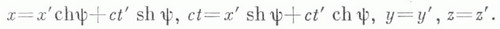
Эти преобразования часто наз. просто Л. п. Они не образуют группу: действие трех гиперболич. поворотов с непараллельными векторами скоростей может дать обычный пространственный поворот - т. н. т о м а с о в с к а я прецессия.

Часто к общим Л. п. добавляют переносы начала координат, получая при этом т. н. преобразования Пуанкаре, образующие группу Пуанкаре.

Свойства группы Л. п. сходны со свойствами ортогональных групп. Отличия связаны с наличием двух типов отражений (пространственных и временных) и с некомпактностью группы Л. п. (т. к. единичная сфера в псевдоевклидовом пространстве, т. е. множество точек, для к-рого модуль интервала до начала координат равен единице, некомпактна).

Физические приложения Л. п. связаны с Эйнштейна относительности принципом, согласно к-рому все физич. законы, кроме законов гравитации, инвариантны относительно Л. п. В ряде случаев, напр. в аксиоматической квантовой теории поля, использование этого и других столь же общих постулатов позволяет делать далеко идущие выводы о видах функциональных зависимостей между различными физич. величинами.

В различных областях физики (в особенности, в теории элементарных частиц) находят широкое применение представления групп Л. п. В соответствии с принципом относительности Эйнштейна физич. величины с различными законами преобразований - векторы, спиноры, тензоры - преобразуются по тем или иным представлениям группы Л. п. При этом оказывается, что эти представления можно характеризовать двумя инвариантами, к-рые отождествляются с массой и спином частиц, описываемых этой физич. величиной.

Инфинитезимальные Л. п., т. е. повороты на бесконечно малый угол, часто используют для получения различных законов сохранения.

Находят применения также Л. п. в касательном пространстве псевдориманова пространства; эти преобразования относятся к т. н. локальным симметриям.

Л. п. получили свое название в связи с работами Г. Лоренца (Н. Lorentz) по электронной теории, к-рые сыграли важную роль в формулировании этого понятия.

Лит.:[1] Л а н д а у Л. Д., Л и ф ш и ц Е. М., Теория поля, 6 изд., т. 2, М., 1973; [2] Н а й м а р к М. А., Линейные представления группы Лоренца, М., 1958; [3] Физический энциклопедический словарь, т. 3, М., 1963. Д. Д. Соколов.