ЛОКАЛЬНО СВЯЗНЫЙ КОНТИНУУМ
- ЛОКАЛЬНО СВЯЗНЫЙ КОНТИНУУМ
континуум, являющийся локально связным пространством. Примеры Л. с. к.: n-мерный куб, n = 0, 1, 2,.. .; гильбертов кирпич;все тихоновские кубы. Объединение графика функции

с отрезком 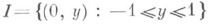 дает пример не локально связного (в точках отрезка I) континуума. Метризуемый континуум локально связан тогда и только тогда, когда ен является непрерывным образом отрезка, т. е. линией в смысле Жордана. Любой метризуемый Л. с. к. линейно связан. Более того, любые две различные точки такого континуума Ксодержатся в простой дуге, лежащей в К.
дает пример не локально связного (в точках отрезка I) континуума. Метризуемый континуум локально связан тогда и только тогда, когда ен является непрерывным образом отрезка, т. е. линией в смысле Жордана. Любой метризуемый Л. с. к. линейно связан. Более того, любые две различные точки такого континуума Ксодержатся в простой дуге, лежащей в К.
В. А. Пасынков.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "ЛОКАЛЬНО СВЯЗНЫЙ КОНТИНУУМ" в других словарях:
КОНТИНУУМ — непустое связное хаусдорфово бикомпактное пространство. К. наз. вырожденным, если он состоит из одной точки. Особо важным является класс метризуемых К. Примеры К.: замкнутый отрезок, окружность, выпуклый многогранник и т. д. Компакт (X, р) (т. е … Математическая энциклопедия
ДЕНДРИТ — локально связный континуум, не содержащий простых замкнутых кривых. Континуум, каждая точка к рого имеет окрестность, являющуюся Д., наз. локальным дендритом. А. А. Мальцев … Математическая энциклопедия
КАКТОИД — локально связный континуум С, к рый является замыканием суммы не более чем счетного числа сфер Si и простых дуг Di, расположенных в евклидовом пространстве Е 3, причем для каждого простого замкнутого контура LМCсуществует одна и только одна сфера … Математическая энциклопедия
ЛИНИЯ — кривая, геометрическое понятие, точное и в то же время достаточно общее определение к рого представляет значитю трудности и осуществляется в разных разделах геометрии различно. В рамках элементарной геометрии понятие Л. не получает отчетливой… … Математическая энциклопедия
Линия (геометрич. понятие) — Линия (от лат. linea), геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. 1) В элементарной геометрии рассматриваются… … Большая советская энциклопедия
Линия — I Линия (от лат. linea) геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. 1) В элементарной… … Большая советская энциклопедия
ДВУМЕРНОЕ МНОГООБРАЗИЕ — топологическое пространство, каждая точка к рого обладает окрестностью, гомеоморфной плоскости или полуплоскости. Д. м. наиболее наглядный класс многообразий: к ним относятся сфера, круг, лист Мёбиуса, проективная плоскость, бутылка Клейна и др.… … Математическая энциклопедия
ДИСК — в топологии поверхность, гомеоморфная кругу, т. е. ориентируемое двумерное, многообразие рода 0 с одной компонентой края. Локально связный континуум без локально разбивающих точек в точности тогда гомеоморфен Д., когда любая окружность вне нек… … Математическая энциклопедия
МЕНГЕРА КРИВАЯ — пример линии, содержащей топологич. образ любой линии (и, более того, любого одномерного метризуемого пространства счетного веса). Поэтому она наз. универсальной кривой. Построена К. Менгером [1] (конструкцию М. к. см. в ст. Линия). М. к.… … Математическая энциклопедия

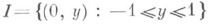 дает пример не локально связного (в точках отрезка I) континуума. Метризуемый континуум локально связан тогда и только тогда, когда ен является непрерывным образом отрезка, т. е. линией в смысле Жордана. Любой метризуемый Л. с. к. линейно связан. Более того, любые две различные точки такого континуума Ксодержатся в простой дуге, лежащей в К.
дает пример не локально связного (в точках отрезка I) континуума. Метризуемый континуум локально связан тогда и только тогда, когда ен является непрерывным образом отрезка, т. е. линией в смысле Жордана. Любой метризуемый Л. с. к. линейно связан. Более того, любые две различные точки такого континуума Ксодержатся в простой дуге, лежащей в К.