- ЛОГИЧЕСКИЕ ИСЧИСЛЕНИЯ
формализации содержательных логич. теорий; выводимые объекты Л. п. интерпретируются как суждения, составленные из простейших (имеющих, вообще говоря, субъектно-предикатную структуру) при помощи пропозициональных связок и кванторов. Чаще всего используются связки "не", "и", "или", "если..., то..." и кванторы существованиях и всеобщности. От произвольных исчислений
Л. и. отличаются чисто логич. характером интерпретаций и правил вывода, от логико-математических исчислений - отсутствием в языке символов конкретных математич. предикатов и функций (за исключением символа
 добавление к-рого интерпретируется как введение в рассмотрение равенства и не считается обычно нарушающим логич. характер исчисления). Сформулированные отличия носят относительный характер, т. к. Л. и. остаются чисто формальными системами, и любая возможная их интерпретация и семантика должны рассматриваться как нечто внешнее, имеющее эвристическую, а не доказательную ценность при научении свойств исчисления.
добавление к-рого интерпретируется как введение в рассмотрение равенства и не считается обычно нарушающим логич. характер исчисления). Сформулированные отличия носят относительный характер, т. к. Л. и. остаются чисто формальными системами, и любая возможная их интерпретация и семантика должны рассматриваться как нечто внешнее, имеющее эвристическую, а не доказательную ценность при научении свойств исчисления.
Одно из важнейших Л. и. - классическое исчисление предикатов с функциональными знаками. Язык этого исчисления, помимо круглых скобок и логич. символов
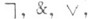
 содержит три потенциально бесконечных списка: список предметных переменных, предикатных переменных и функциональных переменных (каждая из предикатных и функциональных переменных снабжена информацией о своей размерности, причем для предикатных переменных наименьшая размерность 1, а для функциональных - 0). Понятие терма: 1) всякая предметная переменная и всякая функциональная переменная размерности 0 есть терм; 2) если Т 1, ..., Tl - термы, а f - функциональная переменная размерности l, то f( Т 1, ..., Tl).тоже терм. Если Т 1, ..., Т k- термы, а Р - предикатная переменная размерности k, то Р( Т 1, ..., Tk).наз. атомарной ф о р м у л о й. Понятие формулы: 1) всякая атомарная формула есть формула; 2) если Fи G - формулы, а х - предметная переменная, то выражения
содержит три потенциально бесконечных списка: список предметных переменных, предикатных переменных и функциональных переменных (каждая из предикатных и функциональных переменных снабжена информацией о своей размерности, причем для предикатных переменных наименьшая размерность 1, а для функциональных - 0). Понятие терма: 1) всякая предметная переменная и всякая функциональная переменная размерности 0 есть терм; 2) если Т 1, ..., Tl - термы, а f - функциональная переменная размерности l, то f( Т 1, ..., Tl).тоже терм. Если Т 1, ..., Т k- термы, а Р - предикатная переменная размерности k, то Р( Т 1, ..., Tk).наз. атомарной ф о р м у л о й. Понятие формулы: 1) всякая атомарная формула есть формула; 2) если Fи G - формулы, а х - предметная переменная, то выражения

суть тоже формулы. Говорят, что в последних двух формулах все вхождения переменной хсвязанные; вхождения переменных, к-рые в процессе построения формулы не связываются кванторами, наз. свободными вхождениями. Терм Тназ. свободным для хв F, если для любого свободного вхождения хв Fневерно, что оно является вхождением в подформулу вида
 или
или 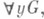 где у - какая-либо из переменных, участвующих в построении
где у - какая-либо из переменных, участвующих в построении 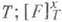 означает результат подстановки Т в F вместо всех свободных вхождений x.
означает результат подстановки Т в F вместо всех свободных вхождений x.
Пусть х - произвольная предметная переменная, А, В, С и D - произвольные формулы, причем Dне содержит хсвободно, Т - произвольный терм, свободный для хв А. Аксиомами рассматриваемого исчисления являются любые формулы следующих 10 видов (каждый из к-рых наз. схемой аксиом):

Кроме того, это исчисление имеет три правила вывода: "из Аи
 можно получить В","из
можно получить В","из 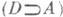 можно получить
можно получить  можно получить
можно получить  ". Доказуемыми формулами (или теоремам и) рассматриваемого исчисления наз. любые формулы, к-рые могут быть получены из аксиом
". Доказуемыми формулами (или теоремам и) рассматриваемого исчисления наз. любые формулы, к-рые могут быть получены из аксиом
исчисления в результате применения (возможно, многократного) указанных правил (см. Вывод логический). Основная интерпретация исчисления предикатов. Область значения предметных переменных - непустое множество предметов М, функциональных переменных - функции из Мв M, предикатных переменных - функции из Мв {0, 1 } (одно из значений интерпретируется как "истина", второе - как "ложь"); имеются в виду функции, определенные на любом наборе предметов, количество членов к-рого соответствует размерности неременной. Теперь для любой атомарной формулы, зафиксировав значение ее предикатной переменной и значения входящих в нее предметных и функциональных переменных, можно говорить об истинности или ложности этой формулы. Аналогично, используя таблицы истинности для пропозициональных связок и обычную интерпретацию кванторов (как бесконечных конъюнкций и дизъюнкций), можно судить об истинности произвольной формулы рассматриваемого языка при выбранном Ми выбранных значениях входящих в нее предикатных, функциональных и свободных предметных переменных. Формула наз. общезначимой, если при любом таком выборе она оказывается истинной. Так, каковы бы ни были значения двуместной предикатной переменной Ри одноместной функциональной переменной f, из того, что для нек-рого хформула P(f(x), f(y)) истинна при любом y, следует, что найдется z, для к-poro P(z,f(z)).истинна. Следовательно, формула

общезначима. Можно доказать, что формула выводима в построенном исчислении тогда и только тогда, когда она общезначима. Приведенная интерпретация опирается на достаточно сложные теоретико-множественные абстракции и поэтому неприемлема с точки зрения нек-рых философий математики и метаматематич. теорий (напр., таких как интуиционизм, финитизм, конструктивная математика). В рамках этих теорий приходится вырабатывать другие представления о семантике Л. и.
Многочисленные Л. и. получаются видоизменением построенного выше Л. и. Так, добавление в язык символа
 вместе со схемами аксиом
вместе со схемами аксиом

(здесь А к Т произвольны, T1 и Т 2 свободны для хв А).приводит к классическому исчислению предикатов с равенством. Выбрасывание из языка функциональных переменных приводит к ч и с т о м у (или узкому) исчислению предикатов. Схемы аксиом 1-8 в сочетании с первым правилом вывода дают классическое исчисление высказываний (т. к. субъектно-предикатная структура суждений не анализируется средствами исчислений высказываний, то обычно вместо различных типов переменных в языке этих исчислений употребляется лишь один Тип - пропозициональные переменные, каждая из к-рых выступает как атомарная формула). Выбрасывание из всех упомянутых исчислений схемы 8 приводит к м и н и м а л ь н ы м Л. и., а схем 7 и 8 - к позитивным Л. и. Возможны и другие частичные Л. и., напр. получившиеся фиксированием части логич. символов или части переменных языка (в сочетании с возможной перестройкой системы аксиом) с сохранением всех классически выводимых формул, составленных из этих символов и переменных; таковы импликативное пропозициональное исчисление (единственный символ
 ), чистое одноместное (сингулярное) исчисление предикатов (в языке содержатся лишь предметные и одноместные предикатные переменные) и др. Наиболее содержательные примеры частичных Л. и. составляют интуиционистские (конструктивные) исчисления, которые получаются из упомянутых классических заменой схемы 8 на схему
), чистое одноместное (сингулярное) исчисление предикатов (в языке содержатся лишь предметные и одноместные предикатные переменные) и др. Наиболее содержательные примеры частичных Л. и. составляют интуиционистские (конструктивные) исчисления, которые получаются из упомянутых классических заменой схемы 8 на схему
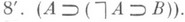
Названия Л. и. естественно складываются из упоминаемых терминов; так, схемы 1-7, 8', 11, 12 определяют интуиционистское исчисление высказываний с равенством.
Рассматриваются также Л. и. с несколькими сортами переменных (и термов), причем не допускаются подстановки термов одного сорта вместо другого. В простых случаях области значения термов разных сортов интерпретируются как разные множества предметов (так, удобные формализации планиметрии могут опираться на Л. и. с предметными переменными двух сортов - "точки" и "прямые"). Но можно последовательно рассматривать сначала исчисление с единственной областью предметов, затем исчисление с дополнительной областью предметов - предикатов над 1-й областью (т. е. во втором исчислении допускаются кванторы по предикатным переменным первого) и т. д. Так возникают Л. и. высших порядков (ранее упоминавшиеся Л. и. имели 1-й порядок). Стремление формализовать логич. теории с более мощным запасом понятий приводит к ряду обобщений Л. <и. Рассмотрение наряду с "истиной" и "ложью" различных степеней неопределенности приводит к различным формализациям многозначных логик и к исчислениям частичных предикатов. Последние Л. и. примыкают к исчислениям логич. следования и строгой импликации исчислению, к-рые возникли в результате попыток формализации реального употребления выражения "из Аследует В" путем снятия парадоксов материальной импликации и отказа от табличного ее задания. Для формализации изучаемого в модальной логике различения "необходимых", "возможных" и "случайных" утверждений служат модальные Л. и. Наряду с заданием Л. и. в терминах схем аксиом часто встречаются формулировки с конечным числом конкретных аксиом, но с добавлением различных правил подстановки вместо переменных. Для многих вопросов теории логического вывода удобны переформулировки Л. и. в виде Генцена формальных систем.
Исчисление вполне адекватно формализуемой теории, если выводимость в нем формулы эквивалентна ее тождественной истинности в основной интерпретации. Истинность выводимых формул связана с непротиворечивостью . (корректностью) исчисления, выводимость всех истинных формул - с его полнотой. Все упомянутые Л. и. корректны, многие из них полны в том или ином смысле (см. Гёделя теорема о полноте). Но, по-видимому, лишь для классич. теорий 1-го порядка достигнута бесспорная адекватность формализации нашим интуитивным представлениям об истинности. Важным свойством Л. и. является разрешимость (см. Разрешения проблема):почти все построенные исчисления высказываний разрешимы; напротив, все упомянутые исчисления предикатов (кроме одноместного) неразрешимы. Для неразрешимых Л. и. тем не менее возможны алгоритмы, к-рые для каждой выводимой формулы устанавливают ее выводимость, но могут не кончать работу для нек-рых невыводимых формул.
Лит.:[1] Гильберт Д., Бернайс П., Основания математики. Логические исчисления и формализация арифметики, пер. с нем., М., 1979; [2] К л и н и С. К., Введение в метаматематику, пер. с англ., М., 1957; [3] Н о в и к о в П. С., Элементы математической логики, 2 изд., М., 1973; [4] Ч ё р ч А.,
Введение в математическую логику, пер. с англ., т. 1, М., 1960; [5] Математическая теория логического вывода. Сб. переводов, М., 1967. С. Ю. Маслов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
