ЛАГРАНЖИАН

функция Лагранжа, интегрант, - подинтегральная функция L(q, q, t )в задаче на экстремум для функционала

экстремальная задача решается при возможном наложении связей и граничных условий; здесь 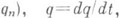L - произвольное дифференцируемое отображение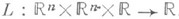

Термин "Л." возник в классич. механике, где в простейшем случае Л. наз. разность кинетической и потенциальной энергии системы, причем движения системы совпадают с экстремалями соответствующего интегрального ф. <ункционала (принцип стационарного действия). В общем случае в классич. механике Л. наз. произвольное дифференцируемое отображение где ТМ - касательное расслоение нек-рого дифференцируемого многообразия М(конфигурационного многообразия системы).

Необходимое условие слабого экстремума функционала (*) при отсутствии связей дается уравнением Эйлера - Лагранжа

Наличие связей типа равенств учитывается при помощи множителей Лагранжа. При наличии "неклассических" связей типа неравенств в теории оптимального управления необходимое условие сильного экстремума функционала (*) дает Понтрягина принцип максимума.

При помощи понятия Л. удобно рассматривать различные симметрии системы, поскольку всякой однопарамет-рич. группе диффеоморфизмов конфигурационного многообразия, сохраняющих Л., соответствует первый интеграл уравнений движения (теорема Нётер).

Во многих задачах полезным оказывается переписать уравнения Эйлера - Лагранжа в виде Гамильтона уравнений, что позволяет, в частности, использовать метод канонич. преобразований и Гамильтона - Якоби теорию. Переход к гамильтоновой форме записи полезен также при квантовании исходной классич. системы. Если Л. не вырожден, то переход к гамильтоновой формулировке производится с помощью Лежандра преобразования, в случае вырождения применяется более сложная процедура редукции (см. [1], [6]).

В механике сплошных сред и квантовой теории поля, к-рые можно рассматривать как механич. системы с бесконечным числом степеней свободы, рассматриваются экстремальные задачи для функционалов вида

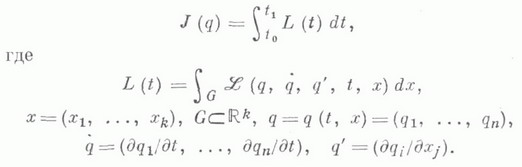
В этом случае функционал L(t).наз. лагранжианом, а функция - плотностью лагранжиана. Основные понятия для таких систем (гамильтониан и др.) вводятся по аналогии с классич. механикой.

Лит.:[1] А р н о л ь д В. И., Математические методы классической механики, М., 1974; [2] Боголюбов Н. Н., Ш и р к о в Д. В., Введение в теорию квантованных полей, 3 изд., М., 1976; [3] И о ф ф е А. Д., Т и х о м и р о в В. М., Теория экстремальных задач, М., 1974; [4] Понтряги н Л. <С. [и др.], Математическая теория оптимальных процессов, 2 изд., М., 1969; [5] С т е р н б е р г С., Лекции по дифференциальной геометрии, пер. с англ., М., 1970; [6] Ф а д д е е в Л. Д., "Теоретич. и матем. физика", 1969, т. 1, № 1, с. 1-18. И. В. Волович.