- ЛАГЕРРА ПРЕОБРАЗОВАНИЕ
интегральное преобразование вида
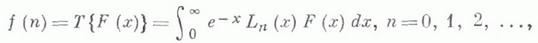
где
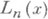- Лагерра многочлен степени п. Формула обращения имеет вид
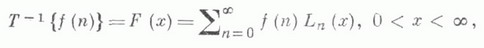
если ряд сходится. Если функция F(x)непрерывна, F' (х)кусочно непрерывна на
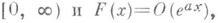
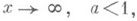то
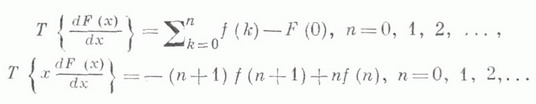
Если функции F(x), F'(x).непрерывны,
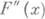кусочно непрерывна на 
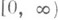и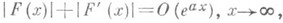 
а<1, то
Если F(х).кусочно непрерывна на
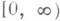и 
то для
Пусть функции F(х).и G(х).кусочно непрерывны на
и
Тогда
Обобщенное Л. п. имеет вид
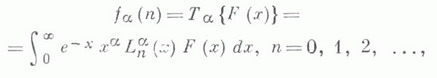
где
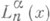- обобщенный многочлен Лагерра (см. [4]). Лит.:[1] 3 е м а н я н А. Г., Интегральные преобразования обобщенных функций, пер. с англ., М., 1974; [2] М с Cully J., "SIAM Rev.", 1960, v. 2, № 3, р. 185-91; [3] D e b n a t h L., "Bull. Calcutta Math. Soc.", 1960, v. 52, № 2, p. 69- 77; [4] Итоги науки. Математический анализ. 1966, М., 1967, с. 7-82. Ю. А. Брычков, А. П. Прудников.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
