КРУЧЕНИЕ

- 1) К. к р и в о й - величина, характеризующая отклонение пространственной кривой 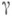от соприкасающейся плоскости. Пусть Р - произвольная точка кривой 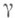и Q - точка кривой 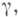близкая Р, - угол между соприкасающимися плоскостями кривой в точках Ри Q, а - длина отрезка PQ кривой Абсолютным кручением 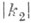кривой 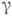в точке Рназ. величина

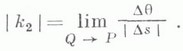
К. кривой определяется равенством 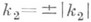и считается положительным (отрицательным), если вращение соприкасающейся плоскости при движении вдоль кривой в сторону возрастания s от вектора бинормали к вектору главной нормали происходит против часовой стрелки (по часовой стрелке) при наблюдении из точки Р.

Регулярная (трижды непрерывно дифференцируемая) кривая в каждой точке, где ее кривизна отлична от нуля, имеет К. Если r=r(s) - естественная параметризация кривой, то

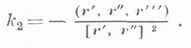
К. иногда наз. второй кривизной. Кривизна и К., заданные как функции длины дуги, определяют кривую с точностью до положения в пространстве. Кривая, у к-рой К. в каждой точке равно нулю,- плоская. Е. В. Шикин.

2) К. геодезическое - обобщение К. кривой, инвариант полосы в пространстве Е ³, определяемый формулой

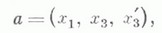
где 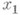- касательный вектор к базовой кривой Г полосы, 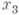- нормальный вектор полосы. Обычное К. 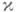кривой Г ненулевой кривизны выражается через а и нормальную и геодезич. кривизны bи спо формуле

Равенство нулю геодезич. К. характеризует полосы кривизны, в частности для полос, принадлежащих поверхности в 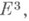- кривизны линии.

Аналогичные понятия вводятся для полос в римано-вом пространстве (см. [1], [2]).

3) К. подмногообразия - обобщение К. кривой, кривизна связности, индуцированной в нормальном расслоении 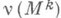многообразия 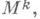погруженного в риманово пространство 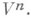Пусть 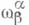- формы связности в 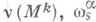- формы эйлеровых кривизн 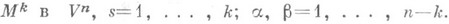Тогда формы

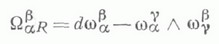
определяют риманово кручение, а формы

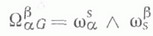
- гауссово кручение 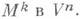Риманово К. и гауссово К. связаны соотношением

где 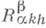- компоненты тензора кривизны Vⁿ в направлении бивектора, касательного к 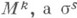- ортогональный кобазис касательного пространства к 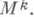Тензоры 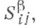получающиеся в разложении форм К.

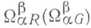по формам 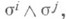нэз. тензорами гауссова и риманова кручения (см. [11,'[4]).

П р и м е р. Пусть М ² - поверхность в евклидовом пространстве Е ⁴. Тогда гауссово и риманово К. равны и сводятся к единственному числу

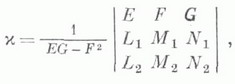
где Е, F, G - коэффициенты первой, а - второй квадратичных форм М ² в Е ⁴. Равенство 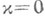в нек-рой окрестности геометрически интерпретируется как вырождение эллипса кривизны в отрезок, тогда существует два семейства ортогональных линий кривизны, касательные к к-рым соответствуют концам этого отрезка. Условие 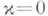локально необходимо и достаточно для того, чтобы М ² располагалась в римановом пространстве V³, погруженном в Е ⁴, и нормаль к М ² в касательном пространстве к V³ была направлена по главному вектору Риччи тензора V³. В частности, нулевое К. необходимо для уплощения М ² в E³.

4) К. аффинной связности Г - величина, выражающая отклонение от перестановочности ковариантных производных какой-либо функции на многообразии М" с этой связностью Г. Она определяется преобразованием

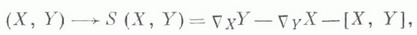
где X, Y - векторные поля на 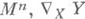- ковариант-ная производная Yвдоль X,[X, Y]- коммутатор Xи У. В локальных координатах 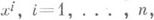таких,

что 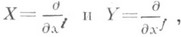преобразование Sимеет вид

тензор 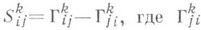- компоненты связности Г в выбранном базисе, наз. тензором кручения.

Эквивалентным образом К. определяется ковариантным дифференциалом векторнозначной 1-формы смещения данной связности

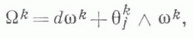
к-рый наз. формой кручения; здесь 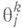- связности формы для Г. В локальном кобазисе 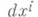(дуальном базису 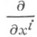) форма

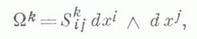
где 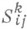имеет те же значения, что и выше.

Геометрич. смысл К. аффинной связности Г заключается в том, что развертка каждого бесконечномалого контура L, выходящего из точки 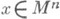и возвращающегося в нее на касательное пространство к М ⁿ в х, уже не будет замкнутой кривой.

Векторная разность между концами развертки с точностью до малых 2-го порядка имеет компоненты Другими словами, этот вектор пропорционален ограниченной контуром Lдвумерной площадке с бивектором Эти представления лежат в основе интерпретации упругой среды с непрерывным распределением источников внутренних напряжений в виде дислокаций, вектор тогда оказывается аналогом так наз. вектора Бюргерса (см. [4]-[7]).

Пример. В двумерном римановом пространстве 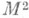с метрической связностью тензор К. сводится к вектору: 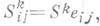здесь 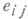- метрич. бивектор. Пусть в ЛЯ дан малый треугольник, образованный отрезками геодезических длины а, b, с, суглами А, В, С. Тогда главная часть проекции вектора 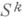в точке Ана сторону АВ равна отношению величины 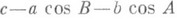к площади треугольника а, а на перпендикуляр к АВ - величине 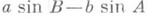, деленной на 0. Таким образом, в М ² нулевого К. имеют место теоремы косинусов и синусов обыкновенной тригонометрии с точностью до величин, малых в сравнении с о.

5) К. пространства А - элемент 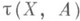Уайтхеда группыWh A, определяемый парой (X, А), где А- конечное клеточное пространство, и вложение 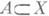является гомотопич. эквивалентностью. Эквивалентно, К.- элемент группы Уайтхеда фундаментальной группы 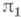. К. инвариантно при клеточных расширениях и стягиваниях и при клеточных измельчениях. Доказана топологич. инвариантность К. Если Аодносвязно, то его К. равно нулю.

Если (W; M₀, M₁) - произвольный h-кобордизм, то 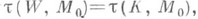где K - клеточное пространство, ассоциированное с данным разложением на ручки многообразия W(от многообразия М ₀), это - кручение h-кобордизма.

Пусть М _f - цилиндр клеточного отображения f: являющегося гомотопич. эквивалентностью. Тогда 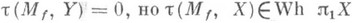не всегда равно нулю. Оно определяет по формуле

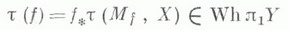
элемент 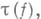наз. кручением отображения f(иногда К. наз. сам 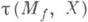). Если 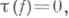то наз. простой гомотопической эквивалентностью (см. [8]).

6) К. конечно порожденной абелевой группы G - группа Т, состоящая из всех элементов конечного порядка v группы G. Числа v>l могут быть однозначно с точностью до перестановки выбраны в виде степеней простых чисел, и тогда они наз. коэффициентами кручения группы G (см. [9]).

Лит.:[1] К а р т а н Э., Риманова геометрия в ортогональном репере, пер. с франц., М., 1960; [2] Б л я ш к е В., Введение в дифференциальную геометрию, пер. с нем., М., 1957; [3] Итоги науки. Алгебра. Топология. Геометрия. 1969, М., 1971, с. 123-68; [4] 3 у л а н к е Р., Винтген П., Дифференциальная геометрия и расслоения, пер. с нем., М., 1975; [5] Н орден А. П., Пространства аффинной связности, 2 изд., М., 1976; [6] К а р т а н Э., Пространства аффинной, проективной и конформной связности, [пер. с франц.], Казань, 1962; [7] Схоутен Я.-А., Тензорный анализ для физиков, пер. с. англ., М., 1965; [8] Р у р к К., Сандерсон Б., Введение в кусочно линейную топологию, пер. с англ., М., 1974; [9] К у р о ш А. Г., Теория групп, 3 изд., М., 1967. М. И. Войцехоеский.