- КОРРЕЛЯЦИЯ
дуальное преобразование,- взаимно однозначное отображение
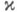 проективного пространства П n на себя такое, что из
проективного пространства П n на себя такое, что из  следует
следует 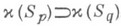 . При К. образом суммы подпространств является пересечение их образов и, наоборот, образом пересечения является сумма образов, в частности образ точки - гиперплоскость, а образ гиперплоскости - точка. Для существования К. пространства П n(K) над телом Кнеобходимо и достаточно, чтобы в Ксуществовал инверсный автоморфизм: взаимно однозначное отображение
. При К. образом суммы подпространств является пересечение их образов и, наоборот, образом пересечения является сумма образов, в частности образ точки - гиперплоскость, а образ гиперплоскости - точка. Для существования К. пространства П n(K) над телом Кнеобходимо и достаточно, чтобы в Ксуществовал инверсный автоморфизм: взаимно однозначное отображение  при к-ром
при к-ром  в этом случае П n (К).оказывается двойственным самому себе. Примерами пространств, для к-рых существует К., являются вещественные
в этом случае П n (К).оказывается двойственным самому себе. Примерами пространств, для к-рых существует К., являются вещественные  комплексные
комплексные  кватернионные
кватернионные 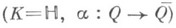 проективные пространства.
проективные пространства.
Пусть ПД интерпретируется как совокупность линейных подпространств (левого) линейного пространства
 над телом К;полубилинейной формой на А п+1 наз. функция
над телом К;полубилинейной формой на А п+1 наз. функция  зависящая от инверсного автоморфизма а тела Ки обладающая следующими свойствами:
зависящая от инверсного автоморфизма а тела Ки обладающая следующими свойствами:

В частности, если
 наз. билинейной формой,- напр., если
наз. билинейной формой,- напр., если  в случае
в случае 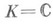 и
и  то
то 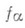 наз. эрмитовой; если же К=Н и
наз. эрмитовой; если же К=Н и  то
то  наз. симплектической. Тогда для любого
наз. симплектической. Тогда для любого  образ К.
образ К.  совпадает с совокупностью решении хуравнения
совпадает с совокупностью решении хуравнения 
(говорят также, что каждая К.
 представима полубилинейной формой
представима полубилинейной формой  - теорема Биркгофа - Неймана).
- теорема Биркгофа - Неймана).
Подпространство Wназ. нулевым относительно К.
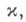 если
если  для любой точки
для любой точки 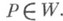 Если
Если  представима формой
представима формой  для всех
для всех  (в частности,
(в частности, ). Напр., строго изотропное подпространство (т. е. подпространство Uтакое, что
). Напр., строго изотропное подпространство (т. е. подпространство Uтакое, что  является нулевым, причем на нем f(U, U)=0; нулевая прямая либо неизотропна, либо строго изотропна. Все максимальные нулевые подпространства К.
является нулевым, причем на нем f(U, U)=0; нулевая прямая либо неизотропна, либо строго изотропна. Все максимальные нулевые подпространства К.  имеют одну и ту же размерность. Если w=П n, то К. наз. нульполярной (нулевой) и является (симплекти-ческим) поляритетом.
имеют одну и ту же размерность. Если w=П n, то К. наз. нульполярной (нулевой) и является (симплекти-ческим) поляритетом.
Обобщение понятия К.- дуальное отображение
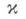 проективных пространств:
проективных пространств:
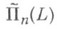 - взаимно однозначное отображение такое, что если
- взаимно однозначное отображение такое, что если 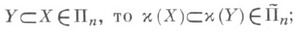 оно существует, если есть инверсный изоморфизм
оно существует, если есть инверсный изоморфизм  Напр., пусть L=K* - совокупность элементов К, в к-рой операции сложения и умножения определены следующим образом:
Напр., пусть L=K* - совокупность элементов К, в к-рой операции сложения и умножения определены следующим образом:  (см. Проективная алгебра, конструкция II). Тогда К* - тело, инверсно изоморфное К;если П n (Х) - левое, то
(см. Проективная алгебра, конструкция II). Тогда К* - тело, инверсно изоморфное К;если П n (Х) - левое, то  - правое проективные пространства, и они канонически двойственны друг другу.
- правое проективные пространства, и они канонически двойственны друг другу.М. И. Войцеховский.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
