КОРРЕЛЯЦИЯ

- зависимость между случайными величинами, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной зависимости К., как правило, рассматривается тогда, когда одна из величин зависит не только от данной другой, но и от ряда случайных факторов. Зависимость между двумя случайными событиями проявляется в том, что условная вероятность одного из них при наступлении другого отличается от безусловной вероятности. Аналогично, влияние одной случайной величины на другую характеризуется условными распределениями одной из них при фиксированных значениях другой. Пусть X и У - случайные величины с заданным совместным распределением весоятностей, т _X и т _Y - математич. ожидания X и Y, - дисперсии X и У, р - коэффициент К. между X и У. Если для каждого возможного значения Х=х определено условное математич. 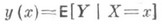ожидание величины У, то функция у(х).наз. регрессией величины Yпо X, а ее график - линией регресси и Yпо X. Зависимость Yот Xпроявляется в изменении средних значений Yпри изменении X, хотя при каждом фиксированном значении Х = х величина Yостается случайной величиной с определенным рассеянием. Для выяснения вопроса, насколько точно регрессия передает изменение Yпри изменении X, используется условная дисперсия Yпри данном значении Х=х или ее средняя величина (мера рассеяния Yоколо линии регрессии)

Если Xи Yнезависимы, то все условные математич. ожидания Yне зависят от x и совпадают с безусловным: 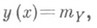при этом 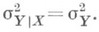При точной функциональной зависимости Yот Xвеличина Yпри каждом данном Х=х принимает лишь одно определенное значение и Аналогично определяется - регрессия Xпо Y. Естественным показателем концентрации распределения вблизи линии регрессии у(х).служит корреляционное отношение

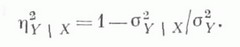
Величина 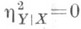тогда и только тогда, когда регрессия имеет вид 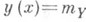, в этом случае коэффициент К. р равен 0 и величина У не коррелирована с X. Если регрессия У по Xлинейна, т. е. линия регрессии - прямая

если, кроме того,|r|=1то Yсвязана с Xточной линейной зависимостью, если же то между Yи Xнет функциональной зависимости. Точная функциональная зависимость Yот X, отличная от линейной, имеет место тогда и только тогда, когда 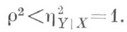Практическое использование коэффициента К. в качестве меры отсутствия зависимости справедливо (за редким исключением) лишь тогда, когда совместное распределение Xи Yнормально (или близко к нормальному распределению), так как в этом случае из равенства r=0 следует независимость Xи Y. Использование r как меры зависимости для произвольных случайных величин Xи Yприводит часто к ошибочным выводам, так как r может равняться 0 даже при функциональной зависимости между величинами. Если двумерное распределение Xи Y нормально, то обе линии регрессии суть прямые и р полностью определяет концентрацию распределения вблизи линий регрессии: при |r|=1 прямые регрессии сливаются в одну, что соответствует линейной зависимости между Xи У, при r=0 величины независимы.

При изучении связи между несколькими случайными величинами X₁... , Х _п с заданным совместным распределением пользуются множественными и частными корреляционными отношениями и коэффициентами К. Последние вычисляются с помощью обычных коэффициентов К. между X_i и X_j, в совокупности образующих корреляционную матрицу. Мерой линейной связи между Х ₁ и совокупностью всех остальных величин Х ₂, ..., Х _п служит множественный коэффициент корреляции. Если взаимосвязь величин Х ₁ и Х ₂ предположительно определяется влиянием остальных величин Х ₃, ..., Х _n то показателем линейной связи между X₁ и Х ₂ при исключении влияния Х ₂,... , Х _п является частный коэффициент корреляции Х ₁ и Х ₂ относительно Х ₂,... , Х _п.

О мерах К., основанных на ранговых статистиках, см. ст. Кендалла коэффициент ранговой корреляции, Спирмена коэффициент ранговой корреляции.

В математич. статистике разработаны методы оценки коэффициентов, характеризующих К. между случайными величинами или признаками, и методы проверки гипотез об их значениях, использующие их выборочные аналоги. Совокупность таких методов наз. корреляционным анализом. Корреляционный анализ статистич. данных заключает в себе следующие основные практич. приемы: 1) построение корреляционного поля и составление корреляционной таблицы; 2) вычисление выборочных корреляционных отношений или коэффициентов К.; 3) проверка статистич. гипотезы значимости связи. Дальнейшее исследование может заключаться в установлении конкретного вида зависимости между величинами (см. Регрессия).

Вспомогательными средствами при анализе выборочных двумерных данных являются корреляционное поле и корреляционная таблица. При нанесении на координатную плоскость выборочных точек получают к о р-реляц ионное поле. По характеру расположения точек поля можно составить предварительное мнение о форме зависимости случайных величин (напр., о том, что одна величина в среднем возрастает или убывает при возрастании другой). Для численной обработки результаты обычно группируют и представляют в форме корреляционной таблицы. В каждой клетке этой таблицы приводятся численности n_ij тех пар ( х, у), компоненты к-рых попадают в соответствующие интервалы группировки по каждой переменной. Предполагая длины интервалов группировки (по каждому из переменных) равными между собой, выбирают центры х _i (соответственно y_i) этих интервалов и числа n_ij в качестве основы для расчетов.

Более точную информацию о характере и силе связи, чем картина корреляционного поля, дают коэффициент К. и корреляционное отношение. Выборочный коэффициент корреляции определяется по формуле

При большом числе независимых наблюдений, подчиненных одному и тому же распределению, близкому к нормальному, близок к истинному коэффициенту К. р. Во всех других случаях в качестве характеристики силы связи рекомендуется использовать корреляционное отношение, интерпретация к-рого не зависит от вида исследуемой зависимости. Выборочное значение 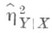вычисляется по данным корреляционной таблицы:

где числитель характеризует рассеяние условных средних значений 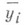около безусловного среднего (аналогично определяется выборочное значение 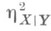). Величина используется в качестве индикатора отклонения регрессии от линейной. Проверка гипотезы значимости связи основывается на распределениях выборочных корреляционных характеристик. В случае нормального распределения величина выборочного коэффициента К. считается значимо отличной от нуля, если выполняется неравенство

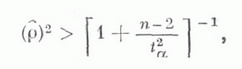
где t_a есть критическое значение t-распределения Стьюдента с ( п-2).степенями свободы, соответствующее выбранному уровню значимости а. В случае 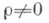обычно используют так наз. z-преобразование Фишера, заменяя величину 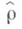на z по формуле

Уже при сравнительно небольших праспределение величины z хорошо приближается нормальным распределением с математич. ожиданием, равным

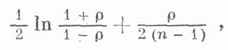
и дисперсией, равной 1/(n-3). Исходя из этого, можно определить приближенные интервалы для истинного коэффициента К. р. О распределении выборочного корреляционного отношения и о способах проверки гипотез о линейности регрессии см. [3].

Лит.:[11 Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975; [2] Ван-дер-Варден Б. Л., Математическая статистика, пер. с нем., М., 1960; ЕЗ] К е н д а л л М., С т ь ю а р т А., Статистические выводы и связи, пер. с англ., М., 1973; [4] А и в а з я н С. А., Статистическое исследование зависимостей, М., 1968. А. В. Прохоров.