КОНТУРНОГО ИНТЕГРИРОВАНИЯ МЕТОД

- один из основных методов геометрич. теории функций комплексного переменного, позволяющий получать различные неравенства, выражающие экстремальные свойства однолистных и многолистных функций, а также тождества, связывающие основные функции областей теории конформного отображения. Метод существенно связан с использованием свойств функций, конформно отображающих данную область на различные канонические области. С помощью таких функций можно строить функции области, обладающие следующим контурным свойством: на каждой граничной компоненте области значения функции разнятся на аддитивную постоянную от комплексно сопряженных значений соответствующей другой функции. К. и. м. состоит в основном в следующем.

Рассматривается нек-рый интеграл, взятый по всему контуру данной области (обычно контур можно считать состоящим из конечного числа простых замкнутых аналитич. ривых). Этот интеграл выбирается так, чтобы подинтегральное выражение содержало множители с указанным выше контурным свойством и чтобы после использования этого свойства получался интеграл, вычисляемый с помощью теоремы о вычетах. Если из других соображений известны либо значение исходного интеграла, либо его знак, то в результате получается или нек-рое соотношение между использованными функциями, или нек-рое неравенство, связывающее их. Часто контурный интеграл, к к-рому удается применить указанный метод, появляется в результате преобразования по формуле Грина неотрицательного двойного интеграла - интеграла от квадрата модуля производной нек-рой функции, регулярной в данной области. Отсюда - связь К. и. м. с площадей методом. С помощью К. и. м. были получены результаты, касающиеся искажения теорем для однолистных конформных отображений многосвязных областей (см. [1], [2]); необходимые и достаточные условия для коэффициентов однолистных функций (см. [3]); тождества, связывающие основные функции областей теории конформного отображения (см. [4]).

К. и. м. применялся для исследования однолистных функций также в следующей форме. Пусть, напр., В- область плоскости wс контуром С, состоящим из конечного числа простых замкнутых аналитич. ривых; S(w)- функция, гармоническая в полной плоскости wза исключением конечного числа точек области В; p(w)- функция, обладающая свойством: разность S(w)- p(w)является гармонической в области Ви непрерывной в этой замкнутой области, p(w)|_C=0. Тогда

где д/дп обозначает дифференцирование по направлению внешней нормали к области В. Если s(w)и q(w)- аналитич. функции, для к-рых S= Re{s},p=Re {q}, то последнее неравенство может быть переписано в виде

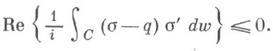
В этом неравенстве интеграл вычисляется по теореме о вычетах. Выбирая различные функции S(w)и p(w), надлежаще связанные с исследуемыми функциями, можно таким образом получать различные новые неравенства для однолистных функций (см. [5] -[7]).

К. и. м. успешно использовался и при исследовании неоднолистных конформных отображений. Так, этим методом был установлен ряд новых экстремальных свойств функций, мероморфных в многосвязной области и удовлетворяющих нек-рым дополнительным условиям (см. [8]); получено обобщение на многосвязные области, на случай нескольких полюсов и на функции, р-листные в соответствующем обобщенном смысле теоремы площадей Голузина для функций, р-листных в круге (см. [9]). Упомянутые выше функции области тесно связаны с Бергмана кернфункциями, и результаты, получаемые К. и. м., часто выражаются через них. Отсюда же следует связь К. и. м. с теорией ортонормальных систем аналитич. функций.

Лит.-[1] Grunsky H., "Schriften math. Semin. und Inst. angew. Math. Univ. Berlin", 1932, S. 95-140; [2] Голузин Г. М., "Матем. сб.", 1937, т. 2, № 1, с. 37-63; [3] Grunsky H., "Math. Z.", 1939, Bd 45, S. 29-61; [4] Gаrаbedian P. R., Schiffer M., "Trans. Amer. Math. Soc", 1949 v. 65, №2, p. 187-238; [5] Nehari Z., "Trans. Amer. Math. Soc", 1953, v. 75, № 2, p. 256-86; [6] Аленицын Ю. Е., "Матем. сб.", 1956, т. 39, № 3, с. 315-36; [7] его же, "Тр матем. ин-та АН СССР", 1967, т. 94, с. 4-18; [8] Меsсhkowski H., "Math. Ann.", 1954, Bd 127, S. 107-29; [9] Аленицын Ю. Е., "Изв. АН СССР. Сер. матем.", ,1973, т. 37, в. 5, с. 1132-54; [10] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966, С. 221 - 26.

Ю. Е. Аленицын.