- КОЛЬЦО
- множество R, в к-ром заданы две бинарные алгебраич. операции: сложение и умножение, причем по сложению это множество - абелева группа (аддитивная группа кольца R), а умножение связано со сложением законами дистрибутивности:
a(b+с) = аb+ас, (b+с) а=bа+са,
где
 На умножение в общем случае не накладывается никаких ограничений, т. е. Rпо умножению - группоид (наз. мультипликативным группоидом кольца R).
На умножение в общем случае не накладывается никаких ограничений, т. е. Rпо умножению - группоид (наз. мультипликативным группоидом кольца R).Непустое подмножество
 наз. подкольцом в R, если Асамо является кольцом относительно операций, определенных в R, т. е. Адолжно быть подгруппой аддитивной группы кольца Rи подгруппоидом мультипликативного группоида этого кольца. Естественно, подкольцами всякого кольца служат само это кольцо и нульподкольцо, состоящее из одного нуля. Пересечение (теоретико-множественное) подколец любого кольца есть подкольцо. Объединением подколец
наз. подкольцом в R, если Асамо является кольцом относительно операций, определенных в R, т. е. Адолжно быть подгруппой аддитивной группы кольца Rи подгруппоидом мультипликативного группоида этого кольца. Естественно, подкольцами всякого кольца служат само это кольцо и нульподкольцо, состоящее из одного нуля. Пересечение (теоретико-множественное) подколец любого кольца есть подкольцо. Объединением подколец  кольца Rназ. пересечение всех подколец, каждое из к-рых содержит все
кольца Rназ. пересечение всех подколец, каждое из к-рых содержит все 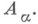 Множество всех подколец данного кольца является решеткой S(R)относительно операций пересечения и объединения подколец. Множество идеалов этого кольца образуют подрешетку в S(R).
Множество всех подколец данного кольца является решеткой S(R)относительно операций пересечения и объединения подколец. Множество идеалов этого кольца образуют подрешетку в S(R).О направлениях в теории колец см. Кольца и алгебры, Ассоциативные кольца и алгебры, Неассоциативные кольца и алгебры.
Р. А. Иванова.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
