КЕЛЛОГА ТЕОРЕМА

пусть функция w=f(z)реализует однолистное конформное отображение круга 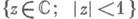на область D, ограниченную гладкой замкнутой жордановой кривой S, у к-рой угол наклона q(l)касательной к действительной оси, как функция длины дуги lкривой S, удовлетворяет условию Гёльдера:

тогда производная f'(z) непрерывна в замкнутом круге а на окружности |z| = 1 выполняются условия Гёльдера с тем же показателем а:

К. т. непосредственно следует из более общих результатов О. Келлога (см. [1], [2]) о граничном поведении частных производных порядков гармонич. функции и(х), являющейся решением Дирихле задачи для области Dевклидова пространства Rⁿ, . ограниченной достаточно гладкой поверхностью Ляпунова S(при ) или кривой Ляпунова S(при n=2; см. Ля пунова поверхности и кривые), причем заданная на границе Sфункция f(у). также предполагается достаточно гладкой.

Другие результаты о граничном поведении производной f'(z)отображающей функции см. в [3], [4].

Лит.:[1] Kellogg О. D., "Trans. Amer. Math. Soc", 1912, v. 13, № 1, p. 109-32; [2] eго же, там же, 1931, v. 33, № 2, p. 486-510; [3] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [4] Warschawski S. E., "Proc. Amer. Math. Soc", 1961, v. 12, p. 614 - 20.

E. Д. Соломенцев.